統計解析と機械学習：要因分析からの考察 Part 1

DataRobotでヘルスケア分野のお客様を担当しているデータサイエンティストの伊地知です。本稿では要因分析に焦点を当て、２回（Part 1、Part 2 ）に渡り考察します。なお、「要因候補となる特徴量」の呼称を以降「説明変数」と統一します。

機械学習は要因分析が得意？

以前書いたブログ中でも言及しましたが、弊社にご連絡をいただくお客様から「機械学習で要因分析をやりたい」とご相談をいただくケースがあります。

そのときに私は「機械学習にとって要因分析は『応用問題』であり、予測や分類を行うのに比べてレベルの高い課題です」と最初にお話した上でご相談に乗るようにしています。

機械学習でY = f(X) のように目的変数Yと説明変数Xの関係を表すモデルが作れたときに、要因分析の文脈では、

• X を増やせばYが増える（or 減る）

と解釈してしまいがちです。（つまり因果関係を想定してしまう）

この過ちは統計モデルの濫用（Abuse）として1966年にウィスコンシン大学マディソン校のGeorge Box教授（1919-2013）が産業界に警鐘を鳴らしたことで知られるようになりました[1]。

実際には機械学習モデルだけから因果関係は分からないので、

• Xが大きければYも大きい（or 小さい）

と、相関関係を前提に解釈するべきです。予測や分類を目的としてモデルを利用するのであれば、このように関係性が分かるだけで十分なのですが、要因分析となると因果関係の検証まで必要になります。その時、機械学習で作られたモデルからは非常に参考になる情報が提供されますが、それだけでは因果関係の検証に十分ではないことを以前のブログでもご紹介しました。

一方、1950年代に統計的品質管理（SQC：Statistical Quality Control）を導入した日本の産業界では伝統的に要因実験（Factorial Experiment）を使った因果関係の検証が行われてきました。つまり、因果仮説の検証を「事前に入念に計画された実験」によって行なってきました。直交表（Orthogonal Array）などを利用した一部実施要因実験（Fractional Factorial Experiment）に代表される実験計画法（DoE：Design of Experiments）の、「最小の労力で最大の情報量を獲得して重要因子とその最適解を探索する」アプローチは「原因と結果」の定量的な因果関係を明らかにするためには最善の方法です。

２因子（品種・施肥量 各3水準）要因実験の例（ある作物の収穫量を計測）

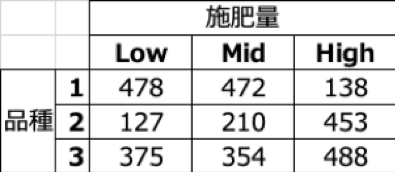
要因実験の課題

実験計画法のような要因実験は数理的に根拠のある手堅い手法ですが、実験で評価対象となる説明変数の数が多くなると指数的に実験回数が増えて現実的な数でなくなってしまう弱点があります。例えば「High」と「Low」の２水準の値をとる変数15個全ての組み合わせを考えると、2の15乗＝32,768通りの実験回数が必要です。

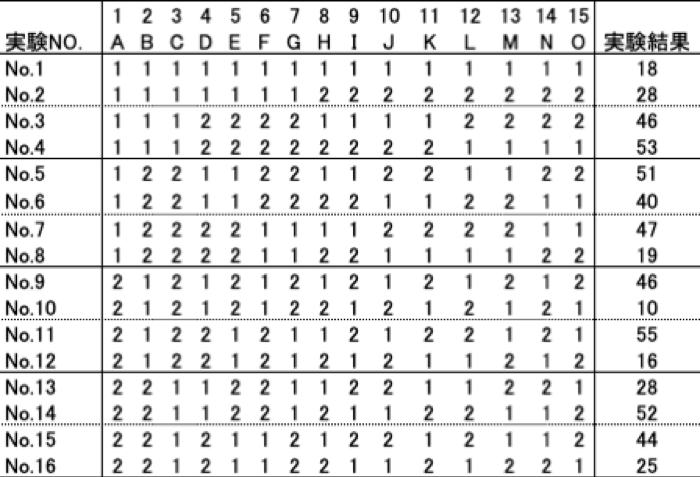
この問題は直交表を利用することで解決できる場合があります。例えば田口玄一博士（1924-2012）が考案したL型直交表L₁₆(2¹⁵)を用いて実験を行い、16通りの実験条件でデータを取得します（下表）。

わずか16回の実験回数でも、もし「交互作用（Interaction）の影響は無視できる」と仮定がおけるなら、15個の要因それぞれの値がLowからHighに変化したときに結果変数へ与える平均的な要因効果を、分散分析（ANOVA：Analysis of Variance）を使って定量的に把握できます。（実験計画法や直交実験、分散分析の詳細は[2]などの書籍を参照ください）

直交表L₁₆(2¹⁵）を利用した実験の例（Lowを1, Highを2で表現）

しかし、評価したい説明変数の数がさらに増え、しかも「High」「Low」だけでなく、もっと細かい水準でデータを取りたい、となったらどうでしょうか？一気に組み合わせ数が爆発して、実際に実験を行うのが現実的でなくなります。（しかも要因実験では「実験順序の無作為化（Randomization）」も行わないといけないため、ますます実験にかかる負担が大きくなります）

したがって筆者の個人的な経験では、あるいは日本品質管理学会誌の報文などを見ても、10個以上の因子（説明変数）を採り上げて実験計画法で要因の探索や因果効果の推定を行なっている事例は少ないです。（一方で、弊社に「数十個あるいは数百個・数千個の説明変数から本当に重要な要因候補の変数を探索したい」というようなテーマでご相談をいただくケースは決して少なくありません）

また、以前のブログでも言及しましたが、医学や社会科学分野では倫理的な観点からそもそも実験を行うことができなかったり、実験を行うためには大きなコスト負担がかかる場合が多いです。そのため、リアルワールドで計測された観察データからの要因分析や、因果関係の探索を行う研究（統計的因果推論[1]など）が発展してきました。

本稿では以降「観察データの解析によって要因分析を行うケース」に目を向けて、下記5つの切り口で考察していきます。

Part 1

• ステップワイズ法のように統計的仮説検定を繰り返す変数選択手法のリスク
• 変数選択プロセスにおけるパーティショニング手法の有効性

Part 2

• 伝統的な多変量解析手法によるアプローチと機械学習を用いたアプローチの適切な使い分け
• 機械学習を用いた変数選択アプローチの限界と、インサイトの安定性・再現性
• 要因分析におけるドメイン知識の重要性

伝統的な多変量解析手法による変数選択のリスク

前述の「要因実験のアプローチでは攻略が難しいケース」は、以下のようにまとめられます。

• 倫理的観点あるいは実験コストの観点から実験の実施が困難なケース
• ドメイン知識の蓄積が少なく、多数の要因候補から何が本当に重要な要因なのかを絞り込むことが困難なケース

これらのケースでは観察データを解析するアプローチによって攻略するしかないわけですが、伝統的な多変量解析の王道である線形重回帰分析を安易に使ってしまうと、以下の2つの間違いを犯してしまうリスクがあります。

• 統計モデルの濫用（Abuse）問題：相関関係を因果関係としてしまう過ち
• 多重検定問題：変数選択（特徴選択）を行なって「強い関係性を持つ少数の説明変数」に絞り込む際に犯す過ち

上記のうち最初の過ちについては既に前々章で述べました。本章では多重検定問題について考察します。多数の説明変数を持つデータを使って、「最も目的変数と関係の強い少数の要因候補」に説明変数を絞り込むケースを考えてみましょう。

1960年代に提唱され、今では各社の統計解析ソフトに標準的に実装されているステップワイズ法は、説明変数を増やしたり減らしたりしながら統計的仮説検定（Statistical Hypothesis Testing）を行なって変数選択を進めるアルゴリズムです[3]。ある統計解析ソフトでは、ボタンをクリックすると10秒も待たずして投入した変数から少数に絞り込まれた分散分析表が現れ、実に簡単に解析結果が返ってきます。

15個の説明変数がステップワイズ法で最終的に3個まで絞り込まれたとします。ステップワイズ法の代表的アルゴリズムである「変数減増法」では説明変数を1個1個減らしたり増やしたりしながら仮説検定を行いますが、仮に15個→3個になるまでに12ステップの仮説検定が行われたとすれば、各ステップでの合計 15+14+13+12+11+10+9+8+7+6+5+4=105回 の仮説検定が実施されることになります。

もし帰無仮説の棄却判断を行う指標（P値）の閾値を最も一般的な5%としていたら、105回の仮説検定作業中に行なった判断（すなわち、ある変数をモデルに取り込むか取り込まないかの判断）が少なくとも1回は間違う確率を計算すると1-0.95¹⁰⁵=0.995 とほぼ100%になってしまいますが、このような問題を多重検定の問題と言います。多重検定により帰無仮説の棄却判断を間違えた場合、本当は目的変数との関係性が認められないのに関係性があると間違えてモデルにその説明変数を取り込む可能性があります。

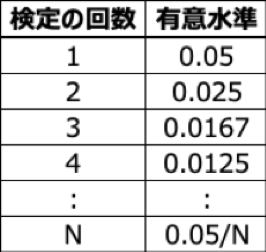
統計的仮説検定の文脈では、このような誤りをαリスクあるいは第1種の過誤、と呼び、産業界では有意水準（P値の閾値）を5%として判断することが一般的ですが、例えば医学研究においては多重検定問題を避けるために「5%を多重検定を繰り返す回数で割った新しい有意水準」で判断を行う方法（Boferroni法）などが使われる場合もあります。（もっとも15個の変数をステップワイズ法で3個に絞り込むため仮説検定にBonferroni法を適用すると閾値を5%から約0.05%にしないといけないので、そもそも重要な説明変数を検知できなくなってしまう可能性があります）

αリスクを5%とした場合の多重検定における有意水準（Bonferroni法による）

繰り返し仮説検定を行う過程のどこかで判断が間違っていたら、最終的に絞り込まれた変数が本当の要因だと自信を持って言えるでしょうか？ちょっと厳しいかもしれませんね。（米国のある大学の医療統計学部では、研究者は「ステップワイズ法を使ったらクビ」と言われていたそうです[4]。人の命に関わる研究でデータ分析結果の再現性が重視されるのは当然で、そのときにステップワイズ法は適切な変数選択手法として認められていないわけです）

20年近く前ですが、SQC方法論を社内で実践し、品質問題の解決に統計解析を利用していた筆者は、当時統計解析ソフトに実装されたばかりだったステップワイズ法を使って数多くの変数から少数の変数に絞り込むアプローチをとったこともありました。今考えるとそのやり方は危険でしたが、後付けで言い訳させていただくならば、5-6個の要因候補に絞り込んでから直交表を用いた実験計画に基づき実際に実験を行なって要因効果を検証しましたので、最終的に間違った判断はしていなかったと思います。しかしそれでも、ステップワイズ法で説明変数を絞り込む過程で重要な要因を見逃すリスクと隣り合わせのアプローチだったと言えるでしょう。

変数選択プロセスにおけるパーティショニング手法の有効性

以上、ステップワイズ法とその手法に伴う多重検定の問題について考察しましたが、では沢山の説明変数がある状況で、適正なアプローチで本当に重要な少数の説明変数（要因候補）に絞り込むにはどうしたら良いでしょうか？医学研究の世界では、解析結果の再現性を担保するために以下のようなデータサンプリング手法を用いた解析アプローチが用いられています[4]。

• 外部データ法：
  – もう1つ別の研究からデータを獲得
  – そのデータを使って同じ方法で説明変数を選択
  – 両者で同じ説明変数が選択されることを示す（=ホールドアウトに該当するデータで再現性を確認する）
• データスプリット法：
  – 1つの研究で得られたデータを2つに分割
  – 片方のデータでモデルに入れる説明変数を選択
  – 2つ目のデータを使って全く同じ方法で説明変数を選択
  – 両者で同じ説明変数が選択されることを示す
• ブートストラップ法：
  – コンピュータ上で「よく似ているけど別の研究のデータ」を仮想でいくつも作成（データの重複を許すブートストラップサンプリングで）
  – それらのデータから全く同じ方法で説明変数を選択
  – 同じ説明変数が選択されることを示す

これらの手法は、機械学習に関心の高い本ブログ記事読者の皆様にはお馴染みでしょう。いずれも機械学習を勉強すると最初に習う汎化性能（未知データに対する予測精度）を評価するためのパーティショニング手法です。確かに、学習データと検定データの両方をバランスよく予測できるようにハイパーパラメータが調整されたモデルであれば、目的変数と関係が深い説明変数のセットは安定している（再現性がある）ことが期待できます。実践手法として、Permutation Importanceの情報を見て逐次的に「説明変数選択〜モデル再構築」を繰り返す方法（下表の③）を弊社山本が以前こちらのブログでご紹介しました。

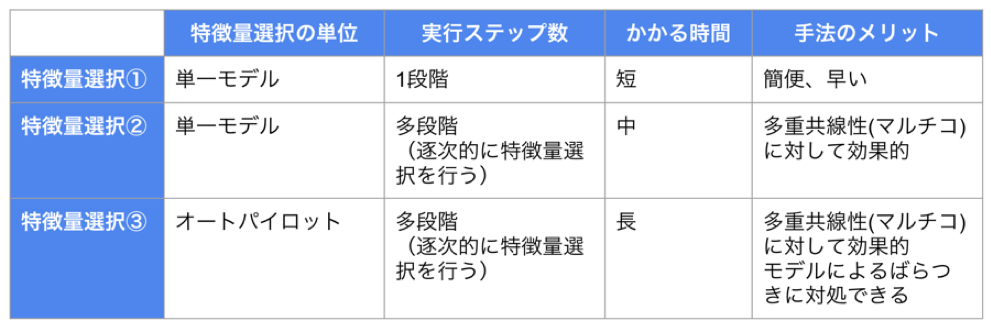
したがって、多数の説明変数から少数の本当に重要な要因候補の説明変数を選択する目的では、元のデータをそのまま100%使ってモデルを作成するのではなく、以下の機械学習のアプローチが、「解析結果（どの説明変数が強い関係性を持っているか）の再現性」を担保する上で、伝統的な統計解析手法では難しい「多数の説明変数を持つデータ」の分析に対しても有効です。

1. 元のデータを分割して交差検定（Cross Validation）などの手法を用いてハイパーパラメータのチューニングを行い、
2. それによってモデルとモデルの複雑度を汎化性能が最大化されるように決定し、
3. その上で目的変数との関係性が強い重要な変数を解析的に明らかにする

DataRobotは学習データ・検定データの適切なパーティショニング、ハイパーパラメータのチューニング、Permutation Importanceを用いたユニバーサルな解析手法による重要変数の表示、を全て自動で行える非常に心強いパートナーだと言えます。

以上、本稿で考察したことをまとめてみます。

• 要因実験は本当に効果のある要因を見つけ因果効果を検証するためのアプローチとしては最善の方法だが、分析対象となる説明変数の数が大きい場合や実験が行えない場合には利用できない。
• 線形重回帰分析に代表される伝統的な多変量解析手法で変数選択を実施するのに、従来統計的仮説検定を繰り返すステップワイズ法などが用いられてきたが、これも説明変数の数が大きいと多重検定の問題により解析から得られる知見（インサイト）の安定性・再現性を担保できない可能性がある。
• 機械学習で汎化性能を確保するために用いられる交差検定などのパーティショニングやハイパーパラメータのチューニングなどのテクニックは、要因分析で必要な「重要な説明変数に絞り込む」解析の結果を安定させるのにも有効である。

次回は、以下の観点でさらに考察を行なって参ります。2020/2/12 に公開予定です。

• 機械学習を応用した要因分析アプローチにも限界がある
• 要因分析で機械学習を使う場合に安定性・再現性のあるインサイトを得るには
• 観察データの要因分析においては、ドメイン知識を駆使しながら伝統的な統計解析と機械学習を適切に使い分けるアプローチが最強

参考文献

[1] 宮川雅巳（2004）：「統計的因果推論 – 回帰分析の新しい枠組み」, 朝倉書店

[2] 永田靖（2000）：「入門 実験計画法」, 日科技連出版社

[3] M. EFROYMSON, Multiple regression analysis, Mathematical Methods for Digital Computers, 1, 191-203 (1960).

[4] 新谷歩（2017）, 「みんなの医療統計 多変量解析編」, 講談社

執筆者について

伊地知晋平（Shinpei Ijichi）

データサイエンティスト

90年代から医療用画像診断装置メーカーで統計解析や機械学習を使った品質改善（シックスシグマ ）、要因分析、異常予兆検知、医療データ分析などに従事。2018年からDataRobot社のデータサイエンティストとしてヘルスケアチームをリードし、主に医療機関や製薬企業でのAIアプリケーション開発をサポートしている。また、伝統的な統計解析手法と機械学習各々の特長を活かした分析アプローチを研究し、各所で講演を行っている。

直近の注目記事
医療でのAI実践、病院で機械学習はどう活用されているのか（ビジネス＋IT）
製薬業界の機械学習活用をプロセスごとに解説、がん治療をAIが助ける？（ビジネス＋IT）

伊地知晋平（Shinpei Ijichi） についてもっとくわしく