モデル最適化指標・評価指標の選び方

DataRobotのデータサイエンティストのオガワミキオです。

5月16日に行った無料セミナーではモデル最適化指標・評価指標について深掘りしました。指標はDataRobotで自動的に選択され、ほとんどの場合には変更する必要はありませんが、各指標の特徴や違い、また目的に応じた使い方を体得することで、更に効果的なモデルを作ることが出来ます。実は指標関連の質問は多くのユーザーさんから今まで寄せられてきました。

なぜ指標を意識する必要があるのか

機械学習モデルをビジネスで利用する上で、最終的に重要なのは事業インパクトです。RoIなどとも言われ、そのモデルの経済効果を表します。機械学習モデルを作る上では、できるだけこのRoIを最大化する必要がありますが、直接的にモデルをRoIに対して最適化するのは現実的ではありません。事業インパクトはモデルのアウトプットからダイレクトに生まれるのではなく、アウトプットを人間が行動や意思決定に利用した結果から生まれるものですし、「こういうモデルを現場で使ったらこういうRoIになった」などというデータはまず存在しないので、直接RoIをターゲットにしたモデルを作ることは多くの場合不可能です。よって、モデル生成・評価は自己完結した指標により、実際のモデル利用とは隔離された条件で行われることが理想的です。今回の記事では、モデル生成のステップのそれぞれにおいて、各指標がどのような役割を担っていて、またどのように関連しているのかを見ていきます。

一つ注意しておきたいのは、正しい指標の選択、は魔法の杖ではないということです。精度の測り方を変えても、良いモデルは良いモデル、悪いモデルは悪いモデルという結果は想像にも難くないでしょう。真にモデルの精度をあげるには特徴量エンジニアリングやハイパーパラメータチューニング、リーケージ除去などから始めるべきでしょう。

機械学習プロジェクトで使われる指標の種類と構造

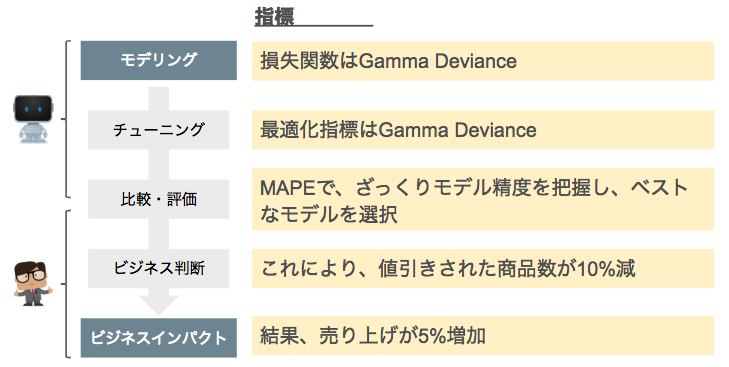
実際にデータから機械学習モデルを作成し、デプロイした効果を測定していくまでのステップにおいては、

1. モデリング
2. チューニング
3. 比較・評価
4. ビジネス判断
5. ビジネスインパクトの計算

のステージに分解でき、ステージごとに別の指標を利用します。各ステージの目的を覚えながら、そこで必要となってくる性質を結びつければ関係性が覚えやすいのでおすすめです。

モデリング

与えられたアルゴリズムと設定において最適なモデルを生成するために損失関数を利用します。モデリングでは、予測値と実測値の誤差（損失）の最適化を行います。損失関数はデータ一件一件に対して計算するため、この後の指標の計算に比べて回数が膨大です。そのため、現代の技術の限界的に数学的に扱いやすい微分可能なものや計算機が計算しやすいものが採用されています。機械学習ライブラリなどを利用している場合は、そのライブラリがサポートしている指標以外を使おうとすると追加の開発が必要になってくるのでコーディングスキルも求められます。ただ新しい損失関数はこれまで歴史上で出たもののマイナーチェンジに近いものも多く、有名どこのライブラリは主要な損失関数をサポートしているので、研究目的でない限りはあまりここに工数を割くのはもったいないと思います。

チューニング

モデルの精度を上げるための最適化指標を利用します。各アルゴリズムのハイパーパラメータの中でもっとも精度の高いモデルを作れる値を、最適化指標を元に探索します。損失関数に比べて全データで一件一件計算するのではなく、できたモデルの精度を最適化指標で測り、ハイパーパラメータ変換して繰り返してと少しは計算量がマシになります。その分、選択の自由度は高いのですが、さすがに閾値を必要とするような指標を選択することは計算量の観点でまだまだできません。

比較・評価

複数モデルを比較して、評価する場合に評価指標を利用します。その際に違うデータセットにおけるこれまでの傾向と比較するためにより解釈性の高いものを選択する場合や、ビジネスKPIに近い閾値を伴った指標を選ぶことが多くあります。

DataRobotにおいては、モデリング、チューニング、比較・評価で使用される指標はオートパイロットでは自動で決定されますが、各パートでマニュアルで設定することもできます。

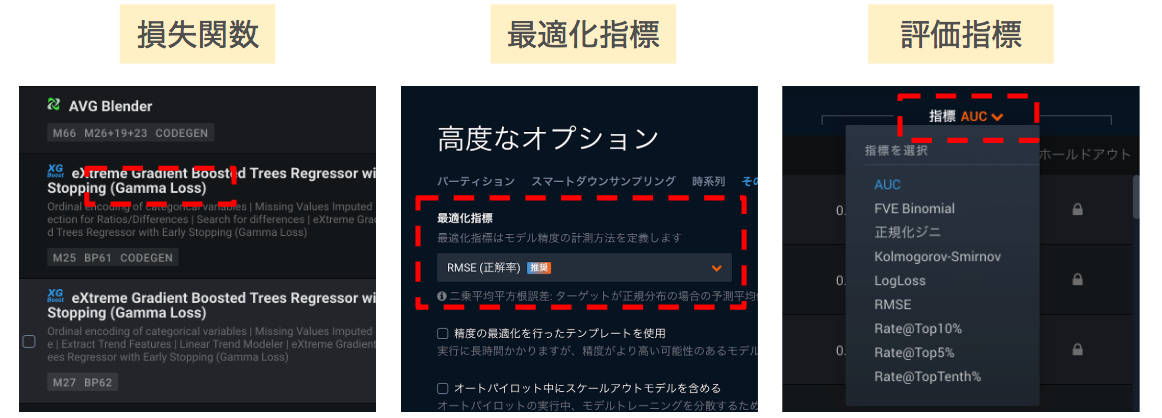
DataRobotは「機械学習の自動化」をメッセージとして掲げていますが、指標の選択というパートにおいても自動化が施されています。注意点としては、DataRobotで自動的に選ばれる指標は最適化指標とUI上はなっていますが、その際に損失関数も選ばれているのです。どの最適化指標で各アルゴリズムでどの損失関数が動いているかも把握できればあなたもDataRobotマニアックマスターに一歩近づきます。

最適化指標と損失関数の組み合わせを暗記するよりも大切なこととして、最適化指標を選択したからといって、それが他の指標を最適化指標に選んだ時よりも必ずいいとは保証されないことがあります。探索の範囲としてスマートグリッドサーチをしているため、局所最適解に陥るケースがあるのです。ただ、あまり大きな違いがでることは少ないので、こういうことが起こるという知識として留めておく程度で良いと思います。

ビジネス判断

モデルをビジネスに適用した際の期待される効果をKPIとして数値化し、実装・実施判断を行います。次のステップのビジネスインパクトの計算と同様であったり、同時に行うケースも多々あります。分析だけをメインで行なっていると、最適化指標でこのスコアが出た！と喜んで終わりのケースをよく見かけますが、その後にビジネス部門でKPIに変換すると大きな変化がなく、リソースのコストの方が高い。。。なんて残念なケースも実はよく見かけるので、分析する側もここの値を意識することはとても大事です。

ビジネスインパクト

最終的なROIを意味していて、実際のモデル運用においてどのような経済効果が出たのかを算出します。コスト減、利益減、売上増と様々な形をとりますが、機械学習プロジェクト全体にかかったコストも反映させる必要があります。全ての機械学習プロジェクトで定量的に測れるものではなく、間接的なインパクトしか算出できないものも存在します。よく機械学習プロジェクトを通年でプランニングする場合には、ビジネスインパクトが測りやすくて出やすいものから始めるように私はアドバイスします。今はAI・機械学習ブーム真っ只中ですが、あれだけヤレヤレ進めていた人も、いざ始まった半年間目に見えない成果が出ないと残念ながら反対勢力に変わります。AI・機械学習でこんなキラキラしたことがしたいと思うのは良いことですが、まずは地味でも成果が出やすい鉄板シナリオをこなし、信頼を築いてからキラキラに取り掛かるのが通年で見ると正解に繋がりやすいものです。

 

連続値回帰問題における指標の一覧

ここからは各指標を具体的に見てみましょう。空で数式が言えるのが偉いのではなく、その性質を知って使いこなすのが大事です。

指標名	特徴	損失関数	最適化指標	評価関数	KPI
RMSE	大きいエラーを重要視する	○	○	△	X
RMSLE	予測と実測の比率と下振れを重視	△	○	△	X
MAE	誤差の幅を等しく扱う	△	○	○	△
MAPE	誤差を百分率で考慮	X	△	○	○
Poisson	離散確率分布	△(BP依存)	○	△	X
Gamma	連続確率分布	△(BP依存)	○	△	X
Tweedie	0か0以外かで	△(BP依存)	○	△	X
R Square	決定係数	X	△	△	X

• RMSE (Root Mean Squared Error)
  
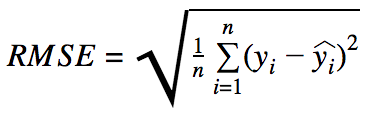
  • 大きな間違いをより重要視
  • 大きな価格の誤差を許容できないケース
  • 損失関数と利用すると平均値に寄りやすくなる
  • 回帰問題においては概ね万能
• RMSLE (Root Mean Squared Logarithmic Error)
   
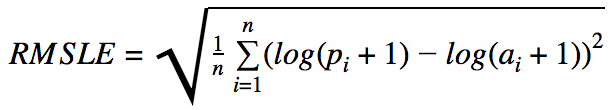
  • 幅ではなく、誤差の割合を重要視
  • かつ上振れよりも下振れを重要視
  • 損失関数として利用する場合には予測値が上振れしやすくなる
  • 小規模のレンジの誤差を重要視したい場合かつ下振れを抑えたいケース
• MAE (Mean Absolute Error)
   
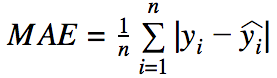
  • 誤差の幅に比例して重要視
  • 平均X予測がずれていると解釈可能
  • 外れ値に対しての重みが弱い
  • 損失関数として利用すると中央値に寄りやすい傾向がある
  • MAEで最適化していくと最大誤差がRSMEに比べて大きくなる傾向
• MAPE (Mean Absolute Percentage Error)
   
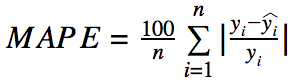
  • 誤差の割合に比例して重要視
  • ターゲットに値が小さいものが含まれるケースには考慮が必要
  • ターゲットに0が含まれていると選択できない
  • 平均X%予測がずれていると解釈可能
• Poisson
   
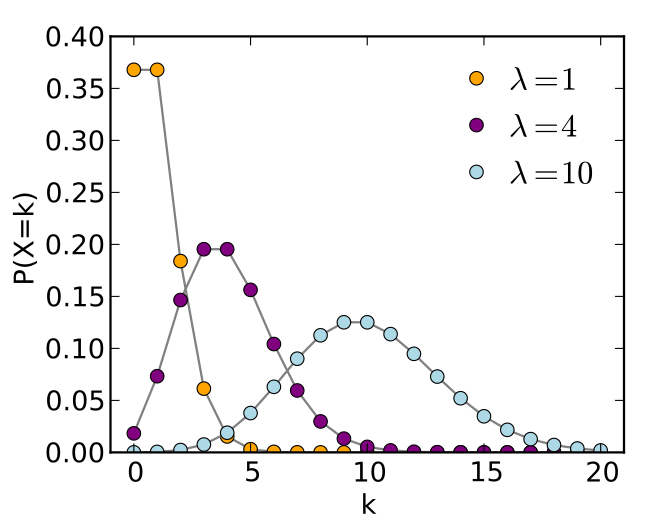
  • 離散的な事象に対しての発生確率
  • 一定区間や一定時間で発生する離散的な事象に対して使用
    • 一定時間の交通量
    • １分間のアクセス数
• Gamma
   
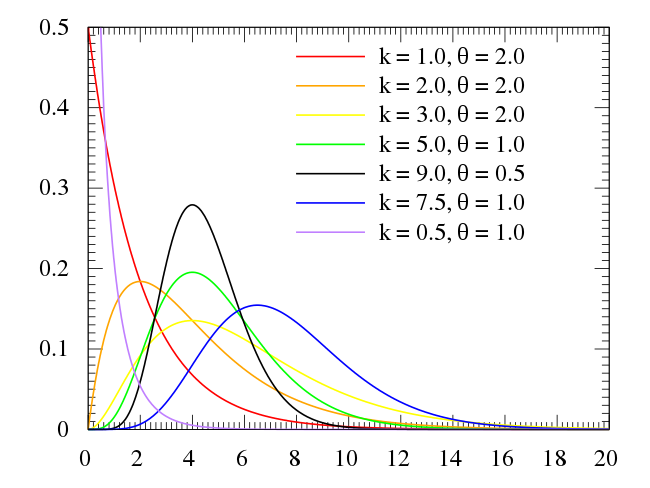
  • 連続確率分布の一種
  • 期間ごとに1回起きる事象がn回起きるまでの時間分布を表す
    • ウイルスの潜伏期間
    • 製品部品の寿命
    • 売上や収入にもよく選択される
• Tweedie
  
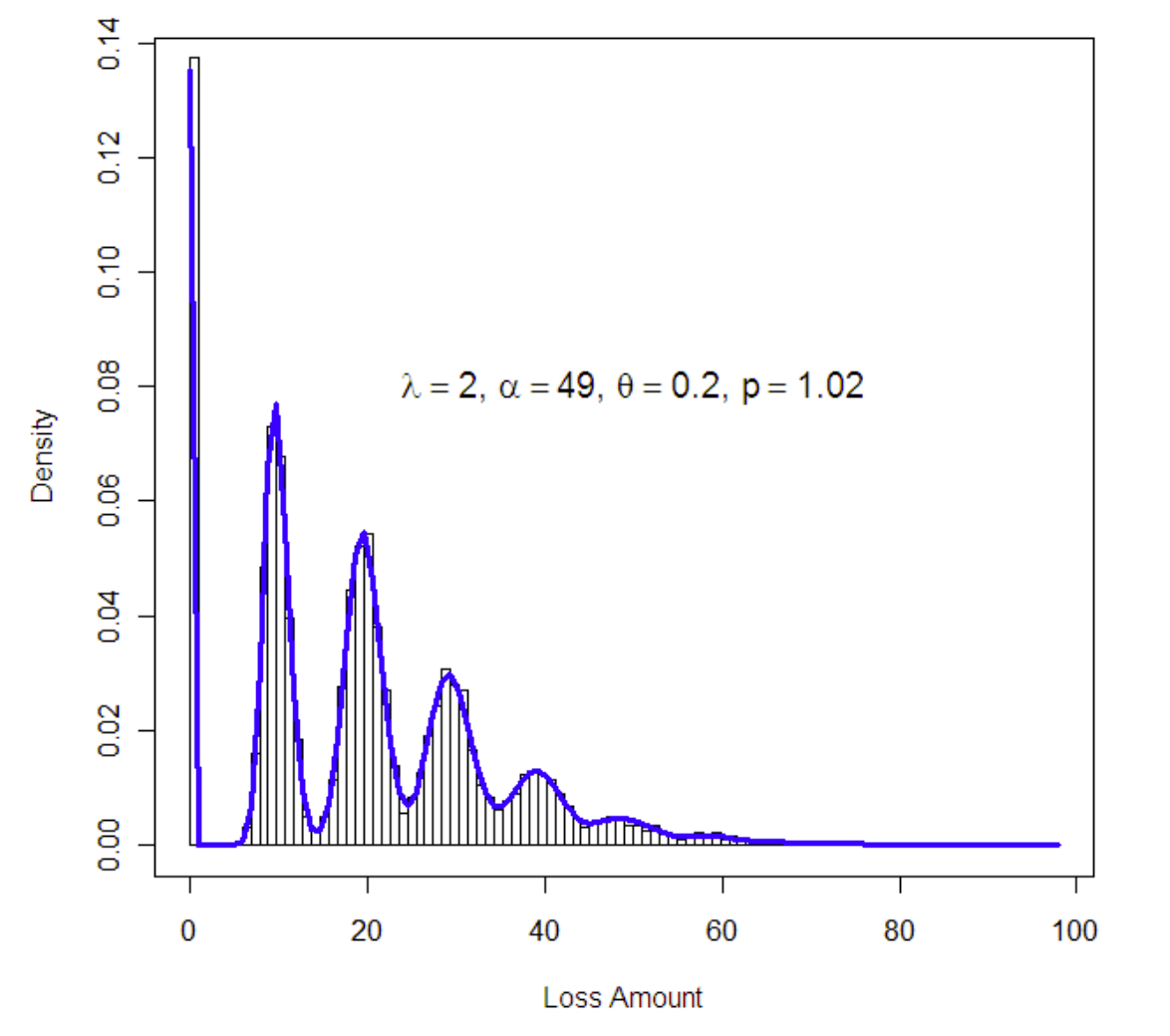
  •  PoissonとGammaを組み合わせたもの
    • 発生回数はPoisson、各事象はGamma
  • ゼロブースト問題において相性が良い
  • ゼロブースト問題
    • 発生しない(0)ことが多いが、発生すると連続値をとるターゲット
    • 保険金支払額
    • 喫煙量
• R Square
  
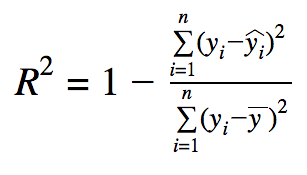
  • 全データが正確に捉えられている場合に、そのままモデルの性能を表すパラメータ
  • データにノイズが多いと勝手にスコアがよくなる傾向
  • DataRobotではアウトオブサンプルで計算

連続値回帰問題だけをとっても様々な指標が存在します。もちろんここに載せていない他の指標も存在しますが、損失関数、最適化指標としてはまずはこのラインナップを覚えれば十分です。ポイントとしては、数式を丸暗記するのではなく、その数式が表したかった事象自体を覚えておくことです。もちろん数式自体の理解が深まれば、ここに出ていない指標を見た際に何を表現しているのか理解しやすくもなります。

 

二値分類問題における指標の一覧

YesかNoを当てる二値分類問題に置いて、単純に何件当たったしかみない人もいますが、YesとNoの比率が極端だとうまく行きません。例えばNoが99%であれば全部Noと言えば、99%当たるわけです。このような状態に陥らない為にも、二値分類でも様々な指標が考えられています。ただ、私は基本的には、LogLossをベースにAUCとPrecision/Recallくらいしか使いませんので、全部はきついという人はそこだけポイントで覚えてみてください。

指標名	特徴	損失関数	最適化指標	評価関数	KPI
LogLoss	エラーの幅も考慮	○	○	△	X
AUC	順位付け	X	○	○	X
Gini Norm / AR	順位付け	X	○	○	X
Kolmogorov-Smirnov	正解数と誤り数の幅を定義	X	○	○	X
RMSE	大きいエラーを重要視する	△	△	△	X
Top X%	上位の精度のみ	X	△	○	△
Precision / Recall	閾値が必要	X	X	△	○

• LogLoss (Logarithmic Loss)
  
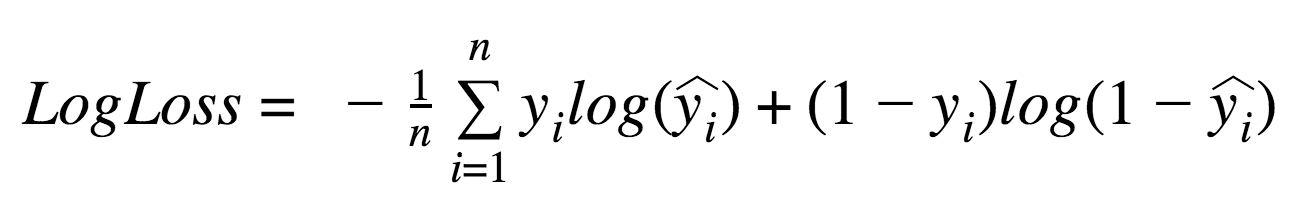
  • 情報理論（エントロピー）に基づく理論的にも扱いやすい指標
  •  実測と予測が乖離しているほどペナルティーが加算
    • 乖離が大きいほどペナルティーは大きくなる（Logで強調される）
    • LogLossが小さいほどモデルの精度が高い
    • 数件でも誤ったラベル付けをしていると罰則が非常に大きい
  • 多値分類でも利用可能
  • Loglossの値で別プロジェクト（別のデータ）のモデルと比較できない
• AUC (Area Under the (ROC) Curve)
  
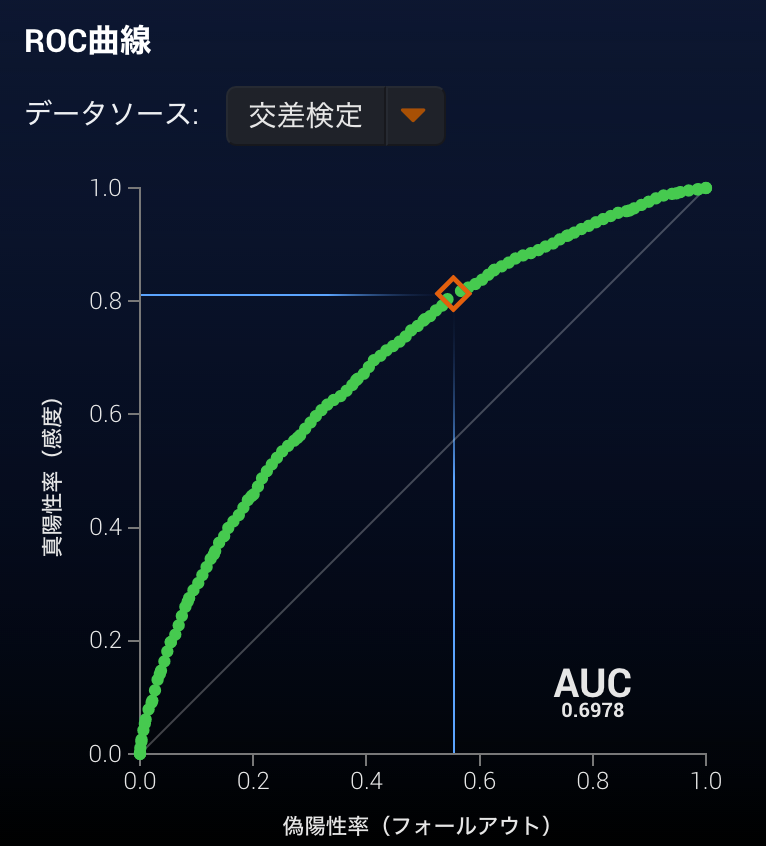
  • ROC曲線(リコールとフォールアウトのプロット)の下の面積
    • 比率を1:1にした場合、ランク付けした際に合っている割合
    • 完全にランダムなモデルの場合でも0.5を取り、1が最も精度が良い
    • 極端にターゲットがアンバランスなターゲットにおいては、モデルの質によらずに高い値を取りやすい
  • 他のモデルとの比較がしやすい
    • わずかな違いは同一のスコアとなる場合がある
• Gini Norm / AR
  
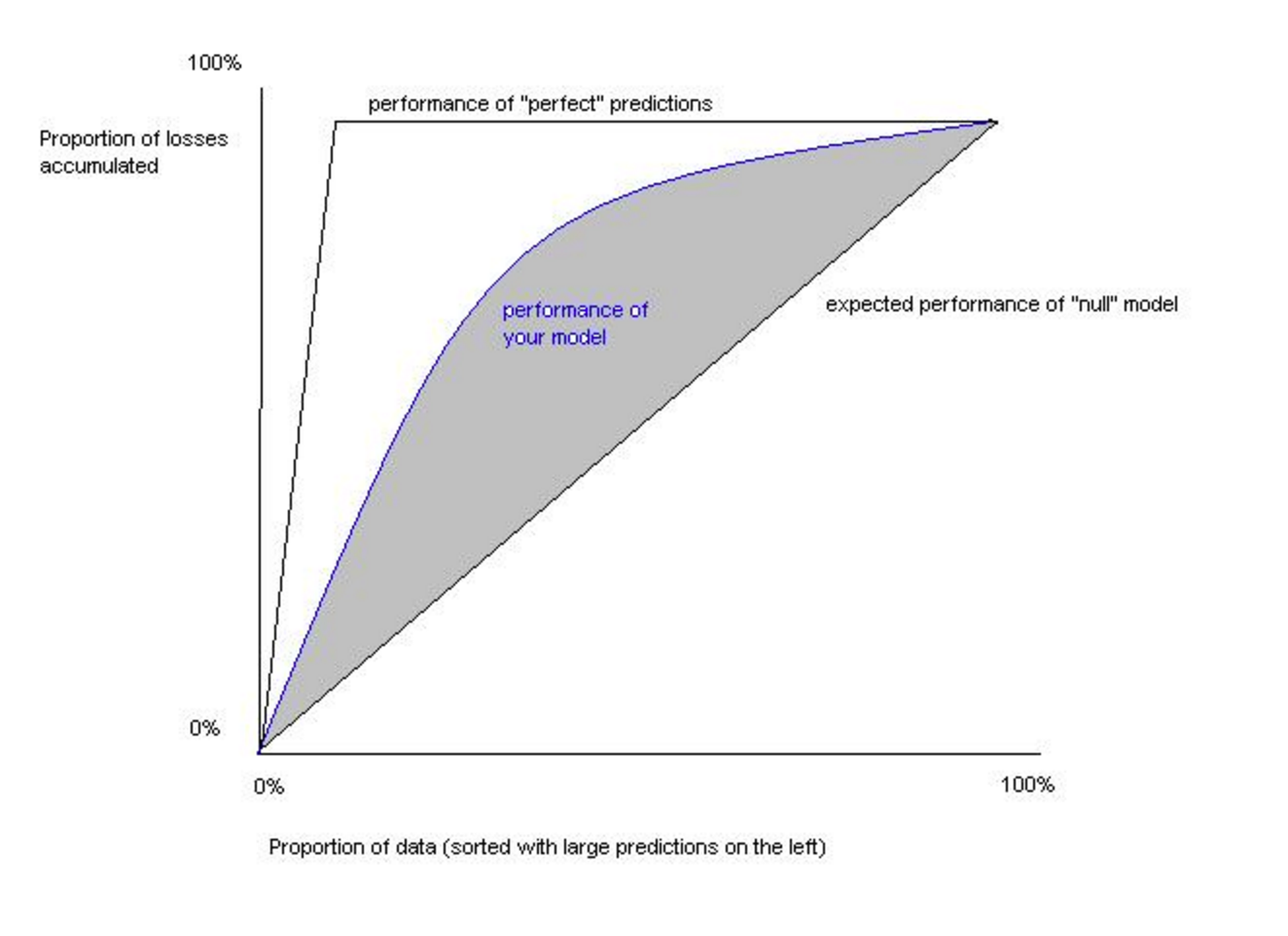
  •  実測値と予測値の順位が正しいかどうかを評価
    • 絶対的な差は考慮しない
  • 二値分類においてはAUCと等価
    • 2*AUC-1：AR値とも呼ばれる
    • 0が最小で1が最大
  • 回帰でも分類でも定義可能
    • 相対的な比較が可能
• Kolmogorov-Smirnov
  
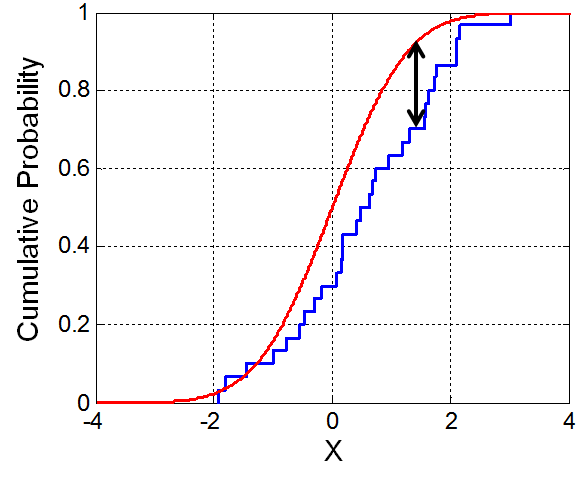
  • 累積確率分布の差を表す
    • 正負の予測分布がよりはっきりと分かれているほど高い値
    • 全く分類できていない予測分布に差異がでない問題では0
  • 金融でよく使われる
• RMSE
  • 大きな間違いをより重要視
  • 大きな価格の誤差を許容できないケース
  • 二値分類問題において正解率を最適化するケースには向いていない
• Precision / Recall
  • 閾値を元に値が変動
  • 予測がどれだけ当たっていたか、実測をどれだけ捉えていたか

二値分類問題における指標を見ていくと、連続値回帰問題で使われていたものがほとんどでなくなってます。ただ連続値回帰問題に比べて選択の幅があるかというと損失関数としても最適化指標としてもLogLossを選んでおけばほとんどのケースで問題ありません。もちろんLogLossにおいては他のデータセットとの比較ができなくなるので、データセットを跨いでのモデルの評価・比較においてはAUCを利用することが多くなります。

また、PrecisionやRecallのように閾値とともに決まっていくものがありますがどう行った閾値に設定するかは、ビジネス用途によって、どんなリスクを取るかによって決まります。閾値によって変動するプレシジョンやリコールをビジネス要件と比較しながらバランスよく選ぶ作業はまだまだ機械には代替できない人間の仕事です。

 

多値分類問題における指標の一覧

指標名	特徴	損失関数	最適化指標	評価関数	KPI
LogLoss	大きいエラーを重要視する	○	○	△	X
Micro Accuracy	全体の正解率	X	○	○	○
Macro Accuracy	各クラスの正解率の平均	X	○	○	△
AUC	順位付け	X	○	○	X

• Micro Average
  • 全体の値
  • クラスごとのデータサイズが影響する
    • 大量に出現するクラスがあり、それが簡単に分類できる場合、値がよくなる
  • DataRobotのAccuracyはMicro
• Macro Average
  • 各クラスの値の平均
  • クラスごとのデータサイズが影響しない
    • 大量に出現するクラスがあり、それが簡単に分類できても値がよくならない
    • 小さなクラスを重要視する場合に利用する
    • 学習データに偏りがある場合に使用する
  • DataRobotのBalanced AccuracyはMacro

ここでも損失関数ではLogLoss最強説は強いですが、最適化指標としては、多値分類問題においてはMicroとMacroの考え方が重要になります。クラスの偏りがあり、全体の正解率を単純に取りたい場合には、たくさんあるクラスを当てれば良いので、Microで問題ないですが、行いたいこととしては、出現頻度が少ないクラスを当てることも重要で各クラスをうまく捉えられていることが重要な場合には、Macroを利用します。

多値分類においては、複数クラスの予測値が順に出力され上から順に選ぶ形となるので、閾値の概念はなくなります。逆に予測値がA 60% B 25% C 5% D 3% E 3% F 3% G 1%とあり、上位三つまで採用すれば正解率はいくつになるといった表現の仕方をすることがあります。

 

DataRobotのデフォルトから変えるべきケース

ここまで様々な指標を見てきましたが、これらを機械学習プロジェクトの性質から適切なものを選択するのは正直大変です。DataRobotの良いところとしては、この指標もターゲットを選択すると自動的に推奨のものを選択してくれる点です。ただ、指標はマニュアルで変えられるようになっていて、いくつかのケースであえて変える場合があるのでそのユースケースにマスターしちゃいましょう。

 

評価の時には必要な指標に変更する

DataRobotのリーダーボードではデフォルトで最適化指標で選んだものが表示されています。LogLossはデータセットが変わると比較ができないのでAUCに変えることが多いです。他にもRMSEは数値だけだと人では解釈できないのでMAPEに変えるといったケースもあります。デフォルトの指標から変えるときはその指標のリスクは押さえておきましょう。よく変更するAUCとMAPEでは、AUCは小さいな変化が捉えられないという欠点がLogLossに比べて存在し、ゼロブースト問題をMAPEに変更すると必要以上に悪いスコアがでるといった性質が知っておかないと突然ハマります。

ちなみにDataRobotとしてモデリング後に評価指標を変更してもモデル自体が再計算されることはないので計算リソースには影響ありませんので、安心してコロコロ変えてみてください。

 

ビジネスケースによって指標を変更する

RMSEでは大きなエラーを重要視する傾向がありますが、ビジネスケースによっては、エラーの幅に関しては等価なこともあります。この場合にはMAEにおいて最適化するほうが望ましいというロジックが成り立ちます。

エラーの幅だけでなく、上振れと下振れに差があるケースもあるでしょう。例えば、売上予測の問題において、在庫リスクと機会損失では在庫リスクのほうがオペレーションに影響が出ることによって影響が大きいことが考えられます。この場合、上振れと下振れを同じに捉えるMAEでなく、RMSLEにおいて最適化するほうが望ましいということになります。RMSLEは性質上、下振れの誤差を上振れに比べて重要視する性質にあるので、全体の予測値が実測値に比べて上にくるケースがありますし、その後にMAEで測ると元のRMSEを最適化指標で選んだモデルよりも精度が落ちているように見えます。ここでも安易に変えるのでは、変える時に起こりうるリスクをしっかりと捉えることが重要です。

実際にRMSEを最適化指標に選んだ時系列の売上予測とRMSLEを最適化指標に選んだ時系列の売上予測を比較して見ましょう。そうすると予測値がRMSLEの方がRMSEに比べて全体的に上に来ていますね。ポイントとしては、元々上に外していたものはもっと外れてしまい、下振れを重要視するといっても完全には防げないという状態です。最適化指標さえ変えれば全てが解けるという期待値は危険で、本当にオペレーション上、下振れが許されないのであれば、予測値にプラスいくつ積むなど運用の仕方でカバーする必要が重要です。

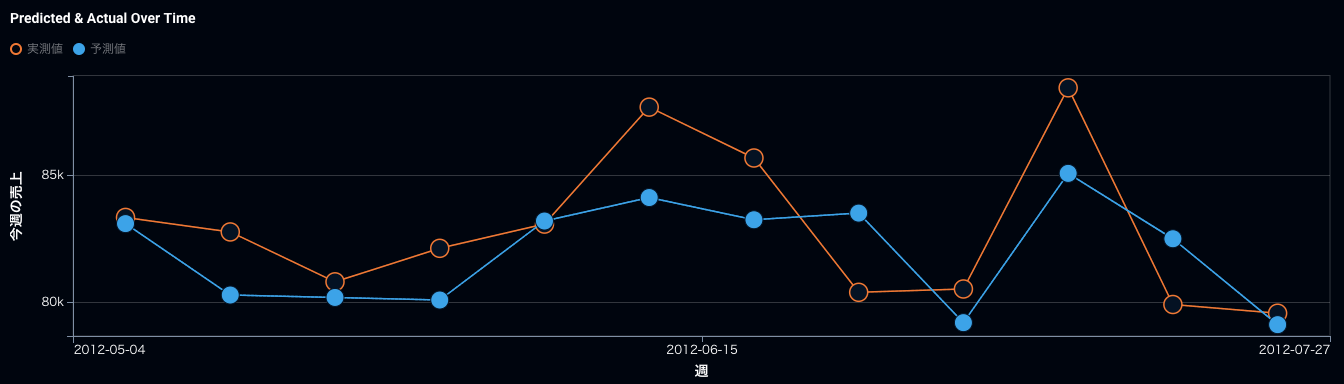
RMSEで最適化した時の時系列での精度。青が予測、オレンジが実測。

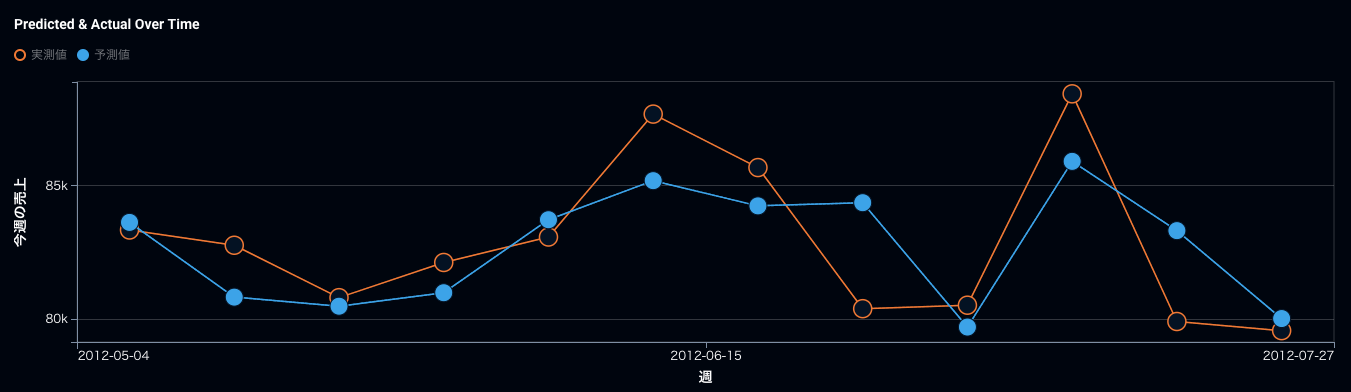
RMSLEで最適化した時の時系列での精度。RMSEに比べて青の予測がオレンジを下回った回数が9回から7回に減っている。

 

コンペでのテクニック

通常の運用であまり気にすることはないですが、0コンマの世界を争うコンペやテーマにおいては、別々の損失関数で作成したモデルをアンサンブルさせるテクニックは有効です。DataRobotにおいては、最適化指標によっては、その時点でいくつかの損失関数を試してみるように動くこともありますが設定可能な全てを網羅的に試しているわけではないので、明示的に損失関数を変更して、アンサンブルモデルを手動で作ることによって、最後ほんのわずかな精度向上に繋がる可能性があります。

イメージとしては、 最終的な比較指標がMAEで合ったとしても、損失関数としてはMAEで作成したモデルとRMSEで作成したモデルをアンサンブルで組み合わせたものを使用します。最終的なアンサンブルモデルはMAEで最適化、評価することによって、元の損失関数としてMAEだけで作られたものよりも精度がよくなる可能性があります。こんな感じのチューニングは楽しいですが、時間をかけすぎて、本来の機械学習プロジェクトの進捗を遅らせないように注意しましょう。

 

答えが明確にわかっているケース

機械学習で扱うデータは多くの場合、現実世界の事象のサンプルに過ぎないのです。交通量の予測をしたい場合にも、毎秒その道路ができてから歴史上全ての交通量が取れているわけではありません。その場合に、真のデータとしての分布と扱うデータの分布が違うケースがあります。

現在取れているターゲットのデータ数では、DataRobotが分布を捉えきれなかったですが、一般的にその事象が特定の分布に従うとすでにわかっている場合には、その分布に設定することによってより未知のデータへの対応力が上がります。

例えば、Poisson分布に従うと言われているものとしては、流れ星の数、交差点の車の数、Webサーバへの１分間のアクセス数などがあり、Gamma分布に従うと言われているものとしては、電子部品の寿命、通信におけるトラフィック待ち時間、所得分布などがあります。

その分野の研究によって、過去に大規模な信頼できる調査が行われており、その事象がその時点から変わっていないケースにおいては有効な手となるのですが、手元のデータはその分布に従っていないわけで、検定スコアでもいい値が出ないかもしれないので、選ぶには勇気がいるケースだと個人的には思います。

 

加重指標の場合

指標を変えるというよりも、指標の計算に対する重み付けを変える方法として、DataRobotにはウェイトという機能があります。特定の商品などを重点的に当てたい場合にはウェイトを指定でき、ウェイトが指定された場合には加重指標が使用されます。単純に全体のウェイト相対から大きな値が付いているウェイトをその値に比例して重要視する（複数回そのデータが出現するように扱う）動作となります。

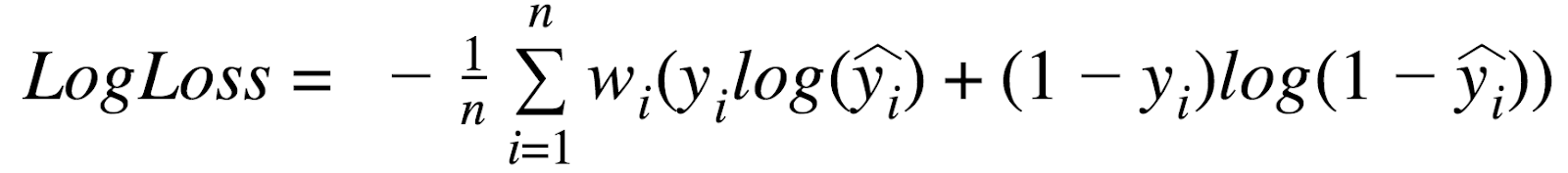
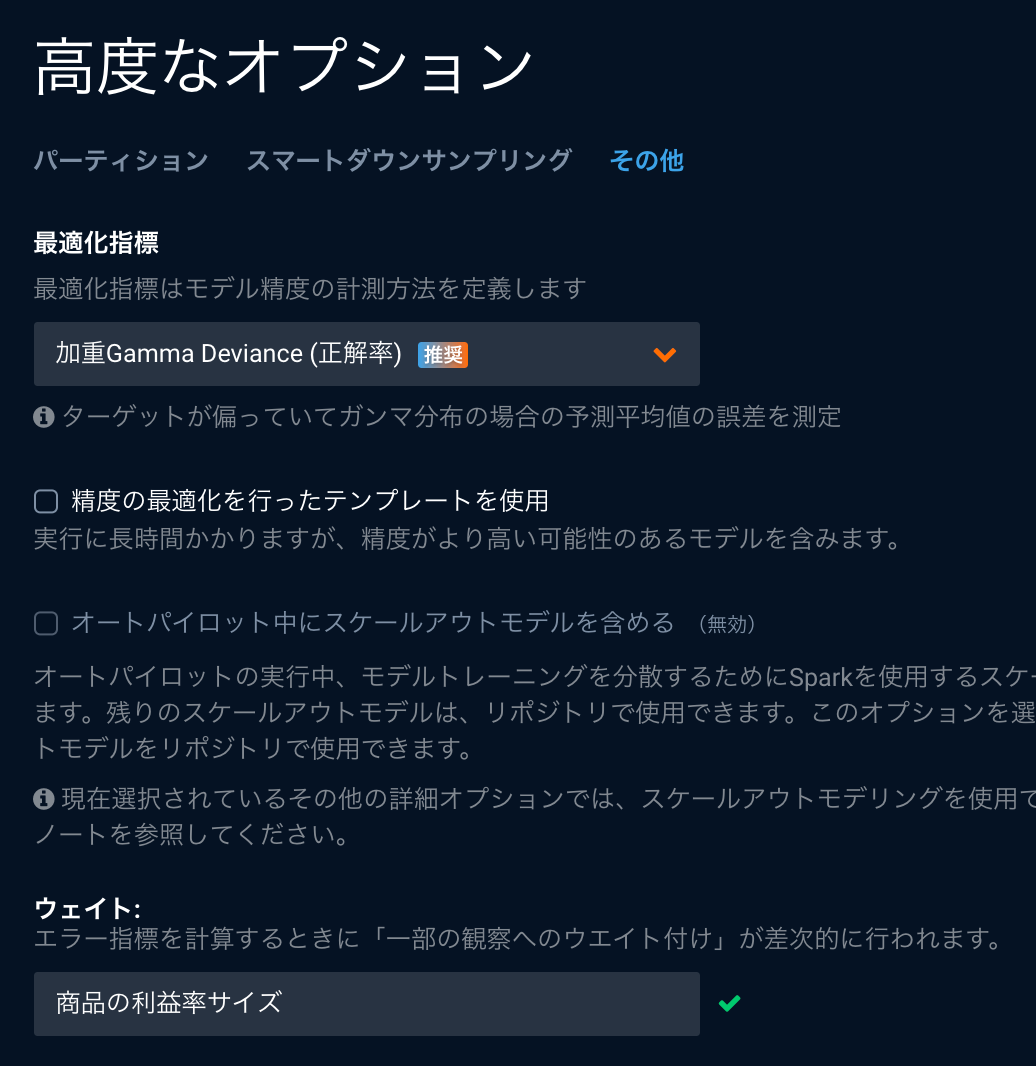
またダウンサンプリングを利用した場合にも、同様に加重指標が使用され、例えば、千行のデータがあったとして、

990がFALSE、10がTRUEである場合

ダウンサンプリングしてFALSEから500行を取り除き、490行のFALSEと10行のTRUEを用いると

class_F_weight = (990 / 1000) / (490 / 500) = 0.99 / 0.98 = 1.0102

class_T_weight = (10 / 1000) / (10 / 500) = 0.01 / 0.02 = 0.5

となります。だいたいFALSE側が内部的に半数になるようにサンプリングしていますが、最終的な重みとしては倍になるようになっていて、補正されています。

この機能もポイントとしては、重みをつけたところを高い確率で当てられるようになるかというと、データの重みを増やしているので、そもそも今のデータセットでは当てづらいような領域であれば精度の向上は大きく認められませんし、逆に他のウェイトが低い部分の精度が落ち込む場合があるので注意が必要です。こだわったわりに大きな効果が出づらいのですが、だからこそ使いこなした時にデータサイエンススーパーヒーローへの道が開けるのです！

まとめ

今回は損失関数、最適化指標、評価指標など普段あまり意識することがない人も多いテーマに付いてピックアップしました。DataRobotは専門性の高い部分も自動化していますが、今回のような知識も持つことによって、より多様なテーマにおいて取り組むことができるようになります。また、指標くらいの数式なら理解してみようと思っていただく方が増えたら個人的に語り合えれる人が増えていいなとも思っています。

続編として、このブログで紹介できなかった筆者の一番のお気に入り指標「FVE Binominal」について書いたブログもぜひご覧ください。