マシューズ相関係数とは – Matthews Correlation Coefficient –

こんにちは。DataRobotの坂本康昭です。今回のトピックはマシューズ相関係数 – Matthews Correlation Coefficient (MCC) – です。これは1975年にバイオケミストのBrian W. Matthewsさんが提案した２値分類モデルの精度をみる指標です。Matthewsさんが発表してから40年以上経った今、DataRobotでも重要な指標のひとつとして使われています。

ここではマシューズ相関係数がどのような指標かご紹介します。メインポイントだけ知りたい読者が多いかもしれませんので先に申しますと、数が少ないクラスを正にする習慣ができている場合はF1スコアやそのベースとなるリコールとプレシジョンといった指標で２値分類モデルの精度を評価いただいて問題ありません。もし機械学習を勉強中で、少数クラスを正とする習慣ができておらず、混同行列なしに指標だけでモデルの精度を評価する時は、F1スコアではなく、マシューズ相関係数をみることをおすすめします。その理由をこれから説明したいと思います。

２値分類問題とは

機械学習でよくある問題のひとつに、データを２つのクラスに分類するというものがあります。例えば、設備が故障するかしないか、患者が再入院するかしないか、顧客がサービスを更新するかしないか、など様々な例があります。このような問題を解くために２値分類モデルを構築した場合、どのようにモデルの精度を測ると良いのでしょうか？

ここではサービス更新の例で考えてみたいと思います。保険や会員制のサービスのように、サブスクリプションという形でビジネスをしていると、既存顧客がサービスを更新してくれるかどうかがビジネス成功への重要な要因となります。特に顧客数が多いと更新率を少しでも上げることができれば大きな利益に繋がります。

多数クラスが正の場合

それでは、100万人の顧客がいて、更新率が90％という想定で、更新率を少しでも上げるために更新するかしないかを予測するリニューアルモデルを生成したとしましょう。ただ、モデルの学習に失敗して、全ての顧客が更新すると予測するモデルが構築されたとします。このようなモデルができたとは誰も気付いていないとしましょう。

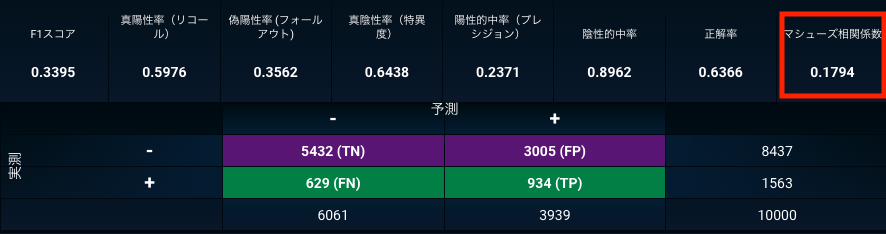
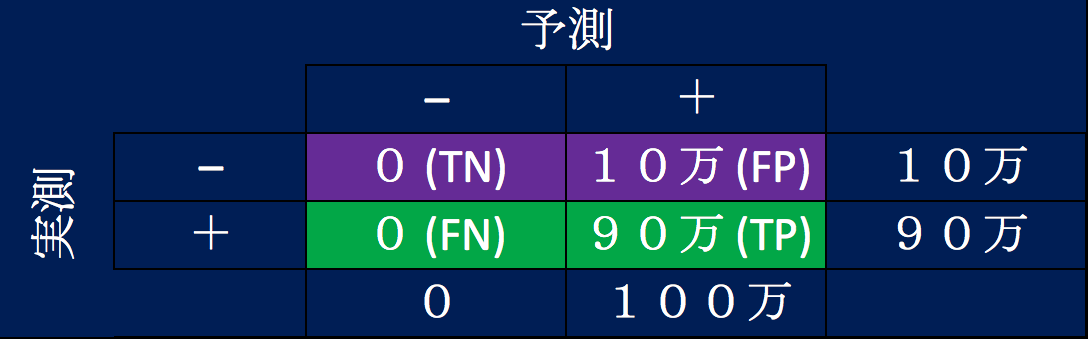
２値分類モデルの精度を理解するひとつの方法は混同行列です。更新率90%で、100万人全員が更新すると予測するモデルの場合、下のようになります。

• 更新すると予測して正解のTrue Positive (TP)は90万人
• 更新すると予測して不正解のFalse Positive (FP)は10万人
• 更新しないと予測して正解のTrue Negative (TN)は0人
• 更新しないと予測して不正解のFalse Negative (FN)も0人

このモデルの精度を正解率で評価してみましょう。90％が更新するので、全員が更新すると予測するモデルの正解率は90％になります。混同行列に基づいた正解率の定義はこちらです。

• 正解率 = (TP + TN) / (TP + TN + FP + FN)

この定義にリニューアルモデルの例を当てはめます。(90万 + 0) / (90万 + 0 + 10万 + 0) = 90万 / 100万 = 0.9となります。90%の正解率という精度の良いモデルができたという判断になりますが、実際は更新しないという予測はしないので、全く役に立たないモデルです。このような理由で、正解率で２値分類モデルの評価をするのは好ましくないというのがわかるかと思います。

それでは正解率以外にどのような評価指標があるのでしょうか？リコールとプレシジョンが２値分類モデルの評価によく使用されます。

まずリコールを見てみましょう。リコールの定義がこちらです。

• リコール = TP / (TP + FN)

今回の例ですと、90万 / (90万 + 0) = 90万 / 90万 = 1となります。実際に更新した顧客を全員更新すると予測したので、リコールは100％となり、リコールで見ても精度が良いという結論になります。

ではプレシジョンはどうでしょうか。プレシジョンの定義はこちらです。

• プレシジョン = TP / (TP + FP)

90万 / (90万 + 10万) = 90万 / 100万 = 0.9となります。100万更新すると予測したうち90万が実際更新したので、プレシジョンは90％です。プレシジョンを使用した評価でも、今回のモデルは精度が良いという結論になります。

リコールとプレシジョンはどちらかを上げようとするともう片方が下がるという関係です。リコールとプレシジョンをバランスよくしようとする指標がF1スコアです。F1スコアのわかりやすい定義は2 x (プレシジョン x リコール) / (プレシジョン + リコール)で、リコールとプレシジョンのハーモニックミーンとなっております。よりシンプル化された定義がこちらです。

• F1スコア = 2TP / (2TP + FP + FN)

今回の例では、180万 / (180万 + 10万 + 0) = 180万 / 190万 = 0.947となります。今回のようにリコールもプレシジョンも高い場合は、F1スコアも高くなります。

今回の、全員更新すると予測するモデルは、正解率、リコール、プレシジョン、F1スコア、全ての指標で精度がよく見えるということになります。しかし、実際は使えないモデルですので、これらの指標は役に立たないということになります。ここで、マシューズ相関係数の出番です。

マシューズ相関係数の定義はこちらです。

• ((TP x TN) – (FP x FN)) / sqrt((TP + FP) x (TP + FN) x (TN + FP) x (TN + FN))

今回の例に当てはめますと、((90万 x 0) – (10万 x 0)) / sqrt((90万 + 10万) x (90万 + 0) x (0 + 10万) x (0 + 0)) = 0となります。

マシューズ相関係数は-1と+1の間の値を取ります。予測と実測が完璧にマッチすると+1、予測と実測が完全に不一致ですと-1、ランダムな予測と同等ですと0という値になります。マシューズ相関係数は混同行列の相関みたいなもので、完璧に当てることができた理想のテーブルと予測結果のテーブルがどれくらい一致しているかを見ています。全問正解でFPとFNが0の場合マシューズ相関係数は1。全問不正解でTPとTNがの場合は真逆な予測でマシューズ相関係数は-1で、予測をひっくり返せばマシューズ相関係数が1になります。

マシューズ相関係数によりますと、今回の全員更新すると予測するモデルは0となり、更新しないとは予測しないので、更新しない方はひとりも正しく予測できず、ランダムなモデルと変わらない精度だという結論です。正解率、リコール、プレシジョン、F1スコアといった指標ではおかしなモデルが完成したと気づくことはできませんでしたが、マシューズ相関係数を見ることによってモデルがおかしいということがわかりました。

少数クラスが正の場合

機械学習の２値分類問題では、正と負の割合が不均衡であることがよくあります。契約更新の例では、更新するという正が多かったですが、逆に正が少なくて負が多いという例がたくさんあります。例えば設備の故障ですと、故障するケースが正で、故障しないケースが負ですが、故障するケースが故障しないケースより圧倒的に少ないことがほとんどです。取引などの不正といった事例も同様で、不正のケースはほとんどなく、不正でないケースばかりということになります。

サービス更新の例に戻りますが、これまでは更新するが正で更新しないが負でしたが、正と負を反転して、更新しないが正で更新するが負という形でモデルを生成することも可能です。リニューアルモデルではなく、チャーンモデルを構築するということです。そうしますと、故障や不正のケースのように、更新せず離脱するという正の数が少なくなり、更新するという負の数が圧倒的に多くなります。

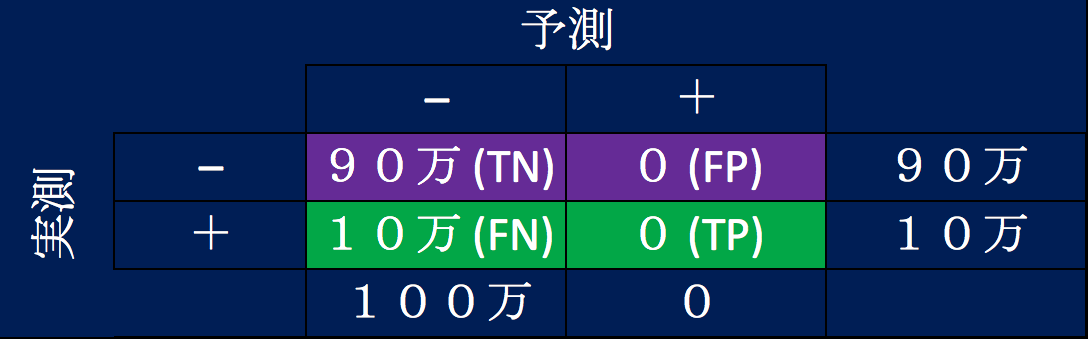
では、また学習に失敗して、全員が更新する、言い換えると離脱しない、と予測するチャーンモデルを生成したと想定して、混同行列を見てみましょう。100万人の顧客がいて、更新率が90％ですので、実際に離脱した数は10万です。

• 離脱すると予測して正解だったTrue Positive (TP)は0人
• 離脱すると予測して不正解だったFalse Positive (FP)も0人
• 離脱しないと予測して正解だったTrue Negative (TN)は90万人
• 離脱しないと予測して不正解だったFalse Negative (FN)は10万人

このチャーンモデルの精度を正解率で評価しますと、(TP + TN) / (TP + TN + FP + FN) = (0 + 90万) / (0 + 90万 + 0 + 10万) = 90万 / 100万 = 0.9となり、リニューアルモデルの場合と同じく90%です。リコールはTP / (TP + FN)ですので、0 / (0 + 10万) = 0となり、プレシジョンはTP / (TP + FP)ですので、0 / (0 + 0) = 0となります。このように、リコールとプレシジョンは正負の反転に影響され、そのためF1スコアも影響され、0となります。チャーンモデルの場合、正解率では精度が良く見えますが、リコールとプレシジョンでモデルがおかしいと気づくことができます。

では、マシューズ相関係数はどうでしょうか。((TP x TN) – (FP x FN)) / sqrt((TP + FP) x (TP + FN) x (TN + FP) x (TN + FN))ですので、((0 x 90万) – (0 x 10万)) / sqrt((0 + 0) x (0 + 10万) x (90万 + 0) x (90万 + 10万)) = 0となります。このように、マシューズ相関係数は、どのクラスが正であるかに依存しません。ですので、マシューズ相関係数は、正のクラスをどう定義するかによってモデルの精度の見え方が変わってしまうF1スコアよりも利点があります。

まとめ

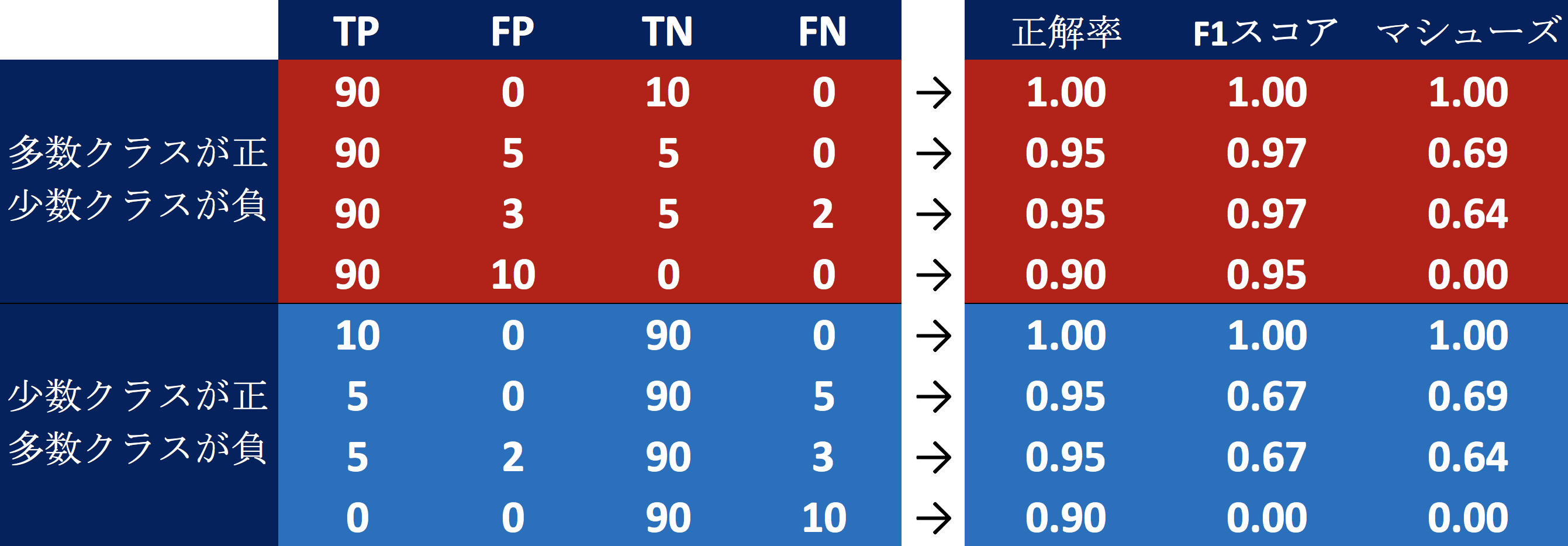
ここで、正負のクラスの定義がどのようにマシューズ相関係数、F1スコア、正解率に影響を与えるかをまとめてみます。

まず、正解率とマシューズ相関係数は正負のクラスの定義に影響されません。正解率は、多数クラスが当たっていれば、少数クラスを完全に間違えても、高くなります。一方で、マシューズ相関係数は、少数クラスで間違えますと、悪くなりますので、多数クラスだけではなく少数クラスも当たらなければ、モデルの精度が良いという結論にはなりません。

逆に、F1スコアは正負のクラスの定義に影響されます。大多数クラスが正で、少数クラスが負の場合は、F1スコアは高く出ます。これは大多数クラスが正ですと、TPがFPとFNと比較して大きくなるからです。少数クラスが正で、大多数クラスが負ですと、TPがFPとFNと比較してあまり大きくならず、F1スコアは低くなります。例えば、大多数クラスが正だった場合F1スコア0.97が、少数クラスが正になった場合、同じ行動をするモデルのF1スコアが0.67まで落ちます。

このように、F1スコアはどのクラスが正であるかによってモデルの精度の見え方が変わりますが、マシューズ相関係数は正のクラスをどう定義するかに依存しません。正と負が不均衡な場合の２値分類モデルの精度を評価する指標としてマシューズ相関係数は最も安全です。

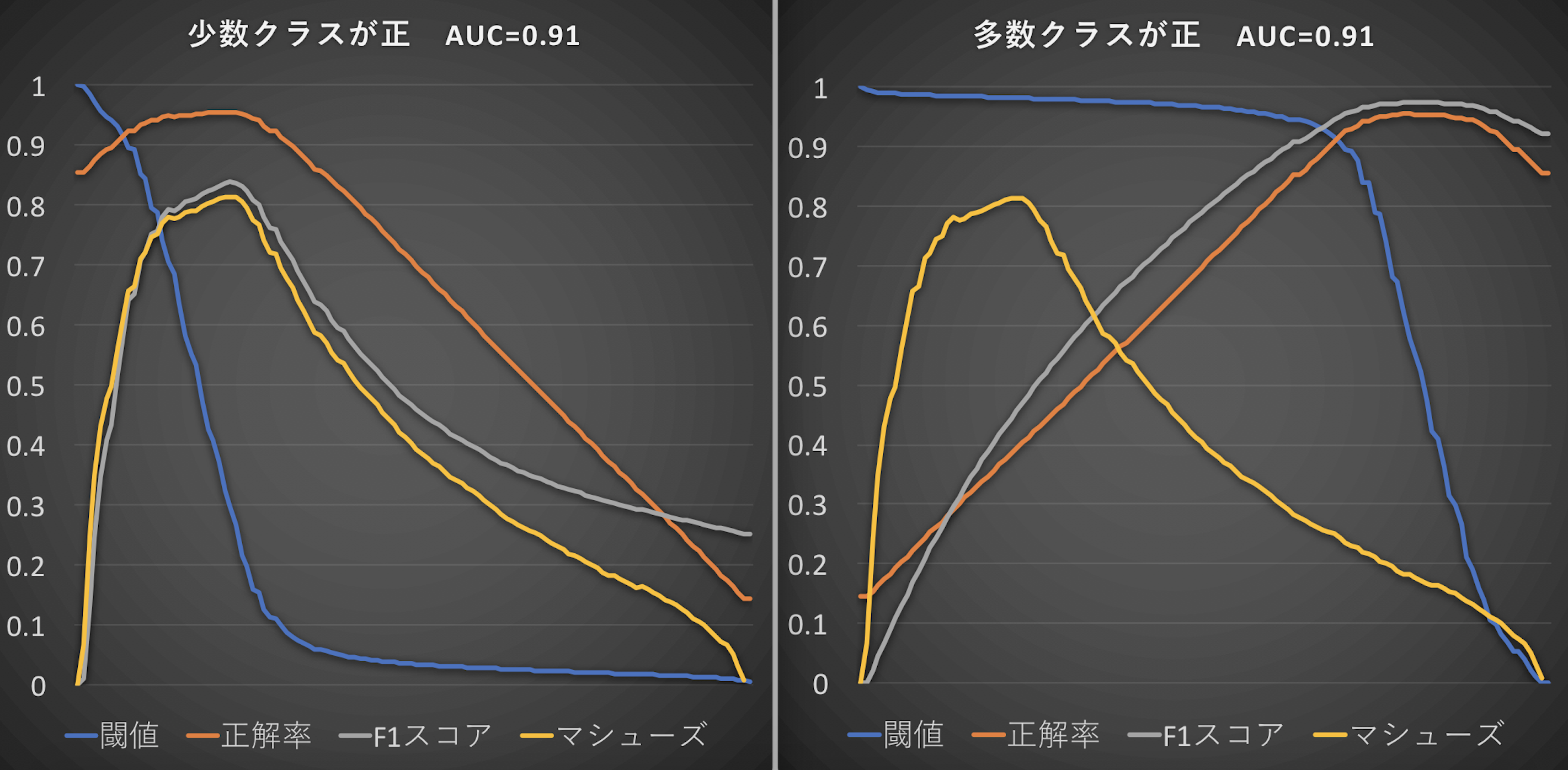
もう少し細かくマシューズ相関係数、F1スコア、正解率の関係性をみてみたいとおもいます。下の図の左側は、少数クラスが正という定義で生成された２値分類モデルの正解率とF1スコアとマシューズ相関係数の関係性を閾値ごとにプロットしたものです。黄色のマシューズ相関係数と灰色のF1スコアが、特に精度が良いところでは、同じような動きをすることがわかります。ここから、少数クラスを正にする習慣ができている場合は、F1スコアやそのベースとなるリコールとプレシジョンで２値分類モデルの精度を評価いただいて問題ない、ということがわかります。

図の右側のパネルは多数クラスが正という定義で生成された２値分類モデルの正解率とF1スコアとマシューズ相関係数の関係性を閾値ごとにプロットしたものです。多数クラスが正の場合は、少数クラスが正の場合とは違い、灰色のF1スコアが、黄色のマシューズ相関係数と似た動きをしておらず、オレンジの正解率と近い動きをしているのがわかります。また、左図と右図でマシューズ相関係数が同じ値を取ることがわかります。

繰り返しになりますが、少数クラスが正の場合はモデル精度の評価にF1スコアとマシューズ相関係数のどちらを使用いただいても問題ありません。多数クラスが正の場合は、F1スコアは正解率のような動きをとりますので、マシューズ相関係数を用いてモデルの精度を評価する必要があります。ですので、何かひとつの指標を使用するのであれば、マシューズ相関係数が最適です。

最後に

DataRobotで２値分類モデルを評価する時、混同行列や予測の分布を使用してF1スコアやリコールとプレシジョンを見ることは多いかと思います。リコールとプレシジョンをバランスよくという意味で、F1スコアがマックスの閾値がデフォルトでは選択されます。DataRobotを使用する上でマシューズ相関係数を見ることはこれまであまりなかったかもしれませんが、学術論文の世界では、正負が不均衡なデータでの２値分類モデルの精度の評価にはマシューズ相関係数を使用するのが一般的です。

ビジネスの世界でもマシューズ相関係数が活躍できるケースがあると思います。これから機械学習を学んでいこうという方。まだ少数クラスを正にする習慣がない場合。混同行列を見ることなく、ひとつの指標だけでモデルの精度を評価する場合。こういった時は、F1スコアではなく、マシューズ相関係数を使用することをおすすめします。

今回のブログではマシューズ相関係数にフォーカスしました。より幅広く評価指標や最適化指標についてご興味がある方は「最適化指標・評価指標の選び方」をご覧ください。

執筆者について

坂本 康昭（Yasuaki Sakamoto）

データサイエンティスト

DataRobot データサイエンティスト。2005年にアメリカの大学にて認知科学博士号取得後、教授職時代にデータサイエンスプログラムの立上げを経験。2015年に日本に戻り、保険会社で AI の応用に従事。2017年から DataRobot のデータサイエンティストとして金融業界のお客様をサポート。

坂本 康昭（Yasuaki Sakamoto） についてもっとくわしく