SHAP を用いて機械学習モデルを説明する

2021/04/14

執筆者:

· 推定読書時間 6 分

はじめに

DataRobot で製造業やエネルギー分野のお客様を担当しているデータサイエンティストの川越雄介です。

機械学習モデルをビジネスや R&D の現場で利用するには、そのモデルがなぜその予測を行ったかや、どのような特徴が効いているかを知ることが重要です。仮に高い精度のモデルができたとしても、例えば営業ターゲティングではなぜその顧客のコンバージョン率が高いと予測されたのかを説明できなければ現場の営業担当者は納得してくれないでしょうし、製造品の不良予測ではそもそも不良要因を特定して製造条件を見直すなどの改善をしなければならないからです。

『AI/機械学習はブラックボックス』と言われがちですが、昨今では「説明可能な AI（Explainable AI: XAI）」という言葉に表されるように、機械学習モデルには解釈性・説明性が強く求められるようになり、それを実現するためのテクニックも世の中に多く出てきています。

DataRobot は、2012年の創業当初から一貫して「説明可能なAI」を重視した製品開発を進めてきました。例えば Permutation Importance を用いた「特徴量のインパクト」、Partial Dependence Plot を用いた「特徴量ごとの作用」、XEMPを用いた「予測の説明」などが実装されています。

【参考リンク】
特徴量のインパクト：ブログ
特徴量ごとの作用：ブログ
予測の説明：ホワイトペーパー（英語）

そして2020年7月からは、SHAP を用いた「特徴量のインパクト」および「予測の説明」が実装されました。この記事では SHAP の概念や計算原理、DataRobot での確認方法を解説するとともに、従来の Permutation Importance や XEMP との使い分けについて考察したいと思います。

シャープレイ値の説明

SHAP（SHapley Additive exPlanations）は、協力ゲーム理論のシャープレイ値（Shapley Value）を機械学習に応用したオープンソースのライブラリです。シャープレイ値をそのまま算出するには、変数の数が増えると組み合わせが増えて計算量が膨大になってしまいます。そこで算出方法を工夫することで現実的な計算時間でシャープレイ値を機械学習で扱えるようにしたものが SHAP です。

SHAP の説明に入る前に、まずシャープレイ値について見てみます。シャープレイ値は、協力ゲーム理論において複数プレイヤーの協力によって得られた利得を各プレイヤーに公正に分配するための手段の一つです。例として、力量の異なる3人のプレイヤー（Aさん、Bさん、Cさん）が協力してゲームに挑戦し、以下の賞金を得るケースを想定します。

A さんは、個人では10万円の賞金を獲得できる。 ①
B さんは、個人では6万円の賞金を獲得できる。 ②
C さんは、個人では4万円の賞金を獲得できる。 ③
A さんと B さんが協力すると、30万円の賞金を獲得できる。 ④
A さんと C さんが協力すると、22万円の賞金を獲得できる。 ⑤
B さんと C さんが協力すると、16万円の賞金を獲得できる。 ⑥
3人が協力すると、60万円の賞金を獲得できる。 ⑦

このケースで、3人で協力して得た60万円の賞金（⑦）をどのように分配すればよいでしょうか？通常は貢献度の高い人に多く分配するのがフェアと考えられます。例えば単純に①〜③に示されている個人の力量を貢献度とし、その比（5 : 3 : 2）で案分すればいいようにも思いますが、それでは④〜⑥に示されている協力の効果が上手く反映されません。個人の力量は確かに A さんが一番大きいですが、もしかするとB さんと C さんの協力による貢献が、もらえる賞金を底上げしてくれているかもしれません。（もちろん、逆に A さんの協力による貢献が大きいこともあるでしょう。）

そこで、「プレイヤーが新たにゲームに加わることにより賞金がいくら増えるか」を表す限界貢献度（marginal contribution）を用いて、A さん、B さん、C さんの貢献を測ります。A さんを例にとると、どの順番で A さんがゲームに加わるかにより、その限界貢献度は異なってきます。

誰も参加しない【賞金0円】→ A さんのみ【賞金10万円】
- A さんの限界貢献度は10万円 – 0万円 = 10万円
B さんのみ【賞金6万円】→ A さんと B さん【賞金30万円】
- A さんの限界貢献度は30万円 – 6万円 = 24万円
C さんのみ【賞金4万円】→ A さんと C さん【賞金22万円】
- A さんの限界貢献度は22万円 – 4万円 = 18万円
B さんと C さん【賞金16万円】→ 3人【賞金60万円】
- A さんの限界貢献度は60万円 – 16万円 = 44万円

B さんと C さんについても同様に全ての順番を考慮し、まとめると以下の図のようになります。

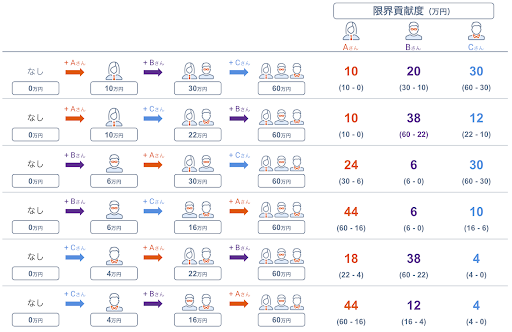
こうして得られた全ての順番における限界貢献度の期待値（平均値）をシャープレイ値といいます。順番の組み合わせは3! = 6通りとなりますので、各個人のシャープレイ値は以下のようになります。

A さん: (10 + 10 + 24 + 44 + 18 + 44) / 6 = 25万円
B さん: (20 + 38 + 6 + 6 + 38 + 12) / 6 = 20万円
C さん: (30 + 12 + 30 + 10 + 4 + 4) / 6 = 15万円

このようにシャープレイ値を用いて報酬を分配することで、各プレイヤーの貢献度に応じた分配ができるようになります。実際に A さんには25万円、B さんには20万円、C さんには15万円が分配され（5 : 4 : 3）、個人の単純な力量比（5 : 3 : 2）で分配するよりも B さんと C さんは多くもらえていますし、かつその合計はちゃんと賞金総額60万円になっています。

シャープレイ値の機械学習への応用（概念）

さて、前項では協力ゲームで得られる報酬をプレイヤーの貢献度に応じて分配しようという考えでシャープレイ値を用いました。この考えを機械学習に適用すると、ひとつひとつの特徴量がモデル予測値に与える貢献度をシャープレイ値で表そうというアイデアが生まれます。

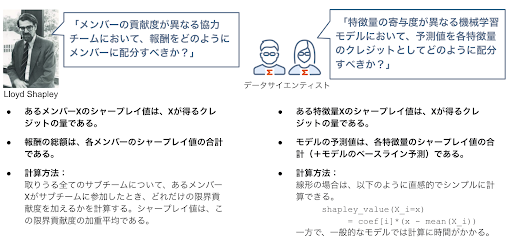
特徴量の数を前項と同じ3つとし、具体的な予測モデルをイメージして述べていきます。あるテーマパークのアイスクリームの売り上げを「気温（z₁）」「湿度（z₂）」「入場者数（z₃）」の3つの特徴量で予測するモデルを作成したとします。仮にある日の気温が30°C、湿度が60%、入場者数が1000人であった時のアイスクリームの売り上げを300個と予測した場合、特徴量である気温、湿度、入場者数がこの予測にどの程度寄与しているかを考えます。

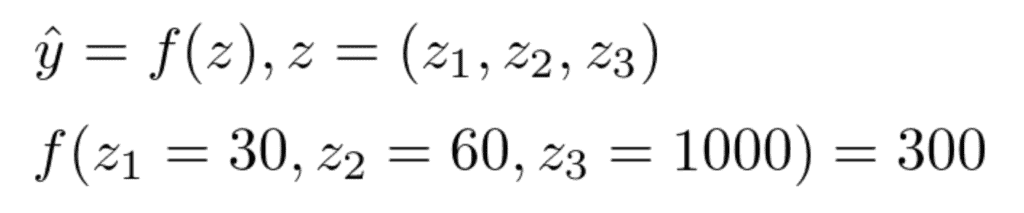
前項のシャープレイ値と同様の発想をすると、例えば、「気温」のみで予測した場合に予測値がどの程度変動するかや、「気温」「湿度」のみでの予測の場合に比べて全ての変数で予測した場合に予測値がどの程度変動するかで、限界貢献度を考えていけばよさそうです。しかしながら、3つの特徴量を使って作成した予測モデルf(z)で、「気温のみで予測」「気温と湿度のみで予測」など、全ての変数が揃っていない場合の予測はどのように表現すればよいのでしょうか。

ここに予測モデルの期待値という考え方を導入します。すなわち平均的な予測値をベースに、ある特徴量が加わったときの予測値の変動量を、その特徴量の限界貢献度としていく考え方です。平均的な予測値をどう決めるかは様々な手法が提案されているようですが、ポピュラーなものは周辺化（marginalization）で、着目しない特徴量が取りうる全ての値での予測の期待値を取るものです。アイスクリームの売り上げ予測を例にすると、何も情報がない場合の予測の期待値（ベースライン）から、気温 → 湿度 → 入場者数の順に確定した特徴量を加えていくと、各特徴量の限界貢献度は以下のようなイメージで示されます。

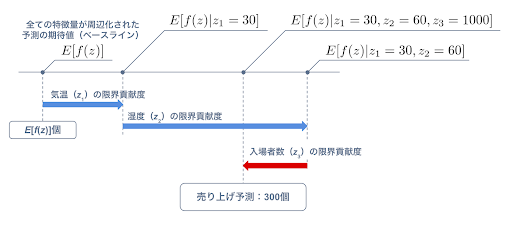
同様に全ての順序の組み合わせで限界貢献度を求め、その平均を取ればシャープレイ値が求まります。このシャープレイ値により、ある予測（z₁ = 30°C, z₂ = 60%, z₃ = 1000人）における各特徴量の寄与が定量的に表現できます。

ちなみに周辺化は、DataRobot では「特徴量ごとの作用」と表示されている部分依存（partial dependence）プロットの計算にも用いられていますので、併せてご参照ください。

SHAP の概要

さて、前項でシャープレイ値の機械学習への応用について概念を説明しました。考え方はシンプルですが、これをまともに計算しようとする場合、特徴量が多いほど計算量は膨大になることにお気づきでしょうか。前項までの例では特徴量は3つしかありませんでしたので、限界貢献度を計算するための順序の組み合わせは 3! 通り、すなわち6通りですみましたが、数が10、20と増えていくと順序の組み合わせは 10! = 約362万通り、20 ! = 2.4 × 10¹⁸通りであり、現実的な時間での計算は不可能です。

そこで近似的にシャープレイ値を算出する手段が SHAP（SHapley Additive exPlanations）です。作者の Scott Lundberg がオープンソースのライブラリとして GitHub に公開しており、世界で人気が高まっています。具体的には、

ツリー系アンサンブルモデルにおける高速で正確なシャープレイ値の算出
ディープラーニングモデルにおける高速で近似的なシャープレイ値の算出
その他の一般的なアルゴリズムにおけるシャープレイ値の推定値の算出

を提供しています。

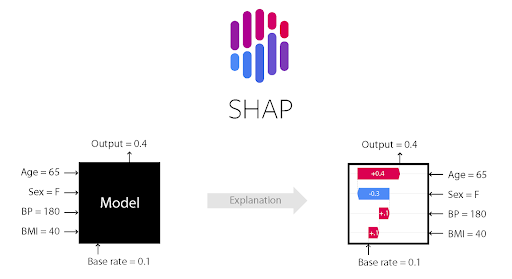
DataRobot も SHAP による「特徴量のインパクト」や「予測の説明」を確認することができます。以降はDataRobot の画面を用いて、SHAP をより詳しく見ていきましょう。

SHAP を用いた予測の説明

DataRobot の「予測の説明」は、予測値に対してなぜその予測を行ったかの理由を説明する機能です。目的はまさにシャープレイ値および SHAP のそれと同じですが、従来の DataRobot では SHAP ではなく、XEMP という手法が用いられてきました。そして昨年のアップデートにより、事前にオプション設定しておくことで SHAP で「予測の説明」を得られるようになりました。（具体的な操作方法については、DataRobot コミュニティのビデオをご覧ください。）

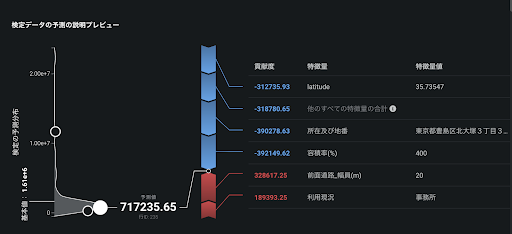
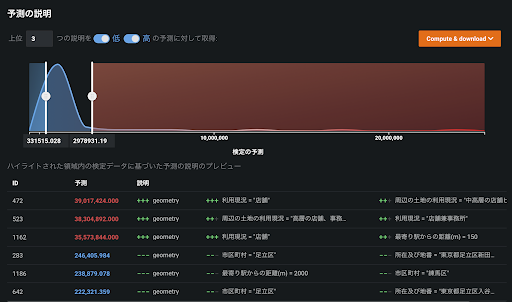
以下のスクリーンショットは、東京23区内の地価を場所や用途等から予測するモデルの「予測の説明」の画面です。あるエリアの地価は、717235.65円/m²と予測されました。この予測モデルの平均的な予測のベースライン（基本値）は、1.61×10⁶円/m²です。そのベースラインに対し、入力条件の「前面道路_幅員(m)」が「20」であることが328617.25円/m²だけ地価の予測値を大きくする方向に、「所在及び地番」が「東京都豊島区北大塚３丁目３（０番１１）」であることが390278.63円/m²だけ地価の予測値を小さくする方向に寄与していることが分かります。

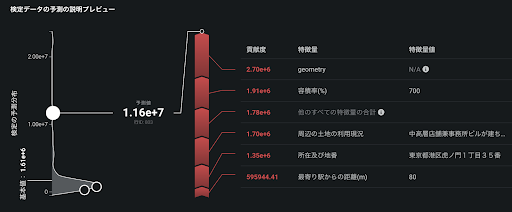
また、以下のスクリーンショットに示されている1.16×10⁷円/m²と予測された別のエリアは、「所在及び地番」が「東京都港区虎ノ門１丁目３５番」であることが地価の予測値を1.35×10⁶円/m²円と今度は大きくする方向に寄与しているのが分かります。東京都豊島区と港区の地価の違いを想像すると、この結果は誰もが納得できるものでしょう。

このように、「予測の説明」は予測結果に説明性や解釈性を与えてくれるため、業務知識や経験と照らし合わせることで納得して予測モデルを業務に適用することができるようになります。これは従来の XEMP でも実現していましたが、SHAP でさらに特筆すべきはその加法性です。前者の豊島区の予測値で説明すると、以下のように平均的な予測値（基本値）を基準にした加法性が成り立ち、その寄与の大きさも比較することができます。まさにシャープレイ値そのものです。

なお、加法性はモデルの直接の出力に対して成立します。上記の場合はモデルの直接の出力をそのまま予測値として用いているので、そのまま加法性が成立しています。一方で、例えば二値分類問題などでは、モデルの出力をリンク関数に通して最終的に0 ~ 1で表される確率空間に変換されます（逆ロジット変換）。この場合はリンク関数に通す前のモデルの出力に対して加法性が成り立つため、DataRobot 画面上は一見して加法性がないように見えますのでご注意ください。

以下の二値分類（ローン融資の貸し倒れ予測）の例では、モデルの出力をロジスティック関数で確率に変換しているため、SHAP の加法性は、逆に基本値や予測値をロジット関数に通した値（= モデルの直接の出力）に対して成立しています。

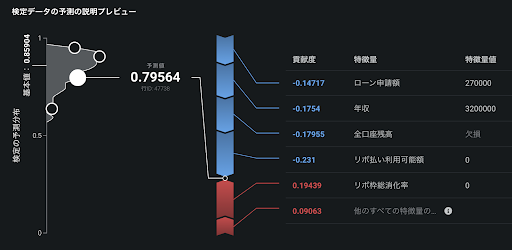
同様に、二値分類に限らず連続値問題においても、DataRobot では精度を高めるためにモデルの出力を変換していることがあります。SHAP の画面で足し算が合わないなと感じたらぜひこの話を思い出してみてください。

SHAP を用いた特徴量のインパクト

前項では、SHAP を用いて1レコードに対する予測の説明を得られることを示しました。1レコード、つまりデータセットにおけるローカルの視点で説明性・解釈性を得たということです。

さらに、他の全てのレコードに対しても SHAP で各特徴量の貢献度を測定することで、機械学習モデルの説明性や解釈性をグローバルにも得ることができるようになります。これは SHAP が基本値（データセットにおける平均的な予測値）および各レコードの予測値の間で、加法性が成り立つように各特徴量の貢献度を得ているからこそです。

DataRobot の SHAP を用いた特徴量のインパクトは、それぞれのレコードで SHAP により得た各特徴量の貢献度の絶対値の平均値をとり、その大小を相対的に比較して表示したものです。これにより、全体的にどの特徴量が予測モデルに効いているかを一目で確認することができます。前述の東京23区の地価予測では「geometry（緯度と経度からDataRobotが自動で作成した地図特徴量）」が最も効いており、順に「周辺の土地の利用現況」「容積率(%)」が効いていることが分かります。

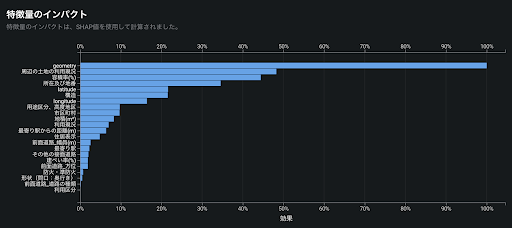
XEMP や Permutation Importance との使い分け

さて、ここまで SHAP を用いた「予測の説明」では1レコードごとの予測に対する各特徴量の貢献度を、そして「特徴量のインパクト」では全体的に予測モデルに効いている特徴量を得られることを説明してきました。

一方で、従来より DataRobot では「予測の説明」では XEMP が、「特徴量のインパクト」では Permutation Importance が使用され、多くのお客様に活用されてきました。では昨年より新たに加わった SHAP は、これら従来の手法とどのように使い分ければよいのか考えていきましょう。

XEMP vs. SHAP（予測の説明）

XEMP（eXemplar-based Explanations of Model Predictions）は DataRobot のデータサイエンティストにより独自に設計され、2016年に初めて導入されました。詳細な算出方法は公開していませんが、ベースラインとなる予測値を持っており、着目する予測において各特徴量がその値を取ることによりベースラインからどの程度変化するかを算出しています。この点は SHAP と同様の考えで設計されていますが、一方で GUI としてはその特徴量が与える予測値の変化の方向と強さを、+ / −の記号と数で表しています。

XEMP は予測モデルに用いたアルゴリズムに依存しない計算方法ですので、DataRobot のあらゆるアルゴリズムに対して算出できます。一方でSHAPはシャープレイ値を近似または推測して求める手法であり、計算できるアルゴリズムが限られるとともに、アルゴリズムによって計算方法も異なります。（DataRobot で SHAP を選択した場合は、本稿執筆時点では線形モデル、ツリー系モデル、およびディープラーニングモデルの一部のアルゴリズムに限られます。）

また、SHAP は XEMP に比べると計算速度がかなり速く、そのため多くの計算結果を短時間で得ることができます。「予測の説明」が得られる特徴量の最大数は、XEMP では10個までに制限していますが、SHAP では（Python SDK を用いると）無制限に取得することが可能です。

その他、XEMP に対する SHAP の長所、短所を以下に示します。

Permutation Importance vs. SHAP（特徴量のインパクト）

Permutation Importance は XEMP と同じくアルゴリズム依存しない計算方法で、当初より DataRobot の「特徴量のインパクト」に採用されています。非常に単純な手法で、ある特徴量を完全にランダムに並び替えて予測させた場合の全体の精度低下を測定しています。ランダムに並び替えられてしまったその特徴量はどんなものであっても予測対象を説明する能力はありません。以下の例のように与信の「貸し倒れ」をターゲットとしてその確率を予測する場合を考えると、与信対象の「信用グレード」という説明力がとても高そうな特徴量であっても、Y さんの「信用グレード」を参考にして全く無関係の X さんの「貸し倒れ」確率を予測できないことは明らかです。この並び替えによる精度低下を全ての特徴量で算出し、低下が大きいものは逆にインパクトが大きいとして算出しています。（詳しい計算方法は別のブログでも解説しています。）

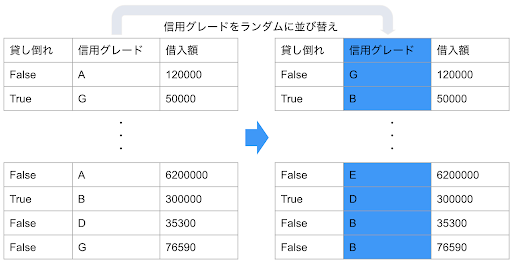
Permutation Importance の「特徴量のインパクト」が SHAP と大きく異なる点は、予測精度の低下を測定しているので、予測対象の実測値、すなわち「正解」を使用しているということです。一方で SHAP は予測値への貢献を各特徴量にどのように配分するかの計算であり、実測値は使用していません。この点をどのように考えるかが、使い分けの大きなキーポイントとなってきます。

考察

SHAP の「使いどころ」については、実は私達 DataRobot のデータサイエンティストの間でも様々なシーンでよく議論対象になります。特徴量選択にはどちらを用いるべきか、モデリング精度向上においてはどうか、モデル運用段階においてはどうかなど、データサイズや特徴量の数、モデルが使われる運用シーンなどによって様々な意見が飛び交うところです。

これまでの議論で筆者がたどり着いた個人的な見解としては、

モデリングの初期段階（教師データの準備や特徴量選択）では、共通の算出方法でどんなモデルでも使用できる XEMP、および実績値を参照して計算される Permutation Importance で分析を進める
ある程度モデリングが進み精度も安定し出したら、SHAP による説明性・解釈性の高さを分析に加えて、さらなる特徴量追加や特徴量エンジニアリングを試みる
最終的には、運用においてモデル精度が必要なのか（一般的に精度が高いのは SHAP が使用できないアンサンブルモデル）、説明性・解釈性の高さが必要なのかによって、運用するものを選ぶ

がよいのではないかと考えています。

もちろん、上記に当てはまらないシーンも多いと思います。私達のある実験では、特徴量選択には Permutation Importance を用いるよりも、SHAP を用いて特徴量のインパクトを測った方が高い精度に早く到達できたという結果もあり、なぜそうであったのか議論や検証が続いているところです。

このように興味が尽きない世界ではありますが、忘れてはならないのは「それが実業務で価値を生み出すかどうか」の視点です。あまり重要でないにも関わらず SHAP の説明性や解釈性の高さに惚れ込んでしまったが故に、アンサンブルモデルなど精度の高いモデルのことを見ずにビジネス価値を目減りさせてしまうことがないよう、それぞれの特性を理解して使うことが大切です。もし SHAP の理解や使い分けが難しいようであれば、DataRobot のデフォルト設定（XEMP および Permutation Importance）のままでもビジネス適用するのには十分と考えます。

まとめ

本記事では、「説明可能な AI（XAI）」として進化を遂げる DataRobot に2020年7月から実装された SHAP について、その計算原理や特徴を詳説しました。また、従来より DataRobot に実装されていた XEMP や Permutation Importance との違いを説明し、使い分けについても考察を進めました。皆様の機械学習モデリングの一助になれば幸いです。

参考

Scott Lundberg氏のオリジナルペーパー、GitHub

Scott Lundberg, Su-In Lee (2017): A Unified Approach to Interpreting Model Predictions
Scott Lundberg, github.com/slundberg/shap; A game theoretic approach to explain the output of any machine learning model.

DataRobot関連資料

Permutation Importanceを使ってモデルがどの特徴量から学習したかを定量化する（DataRobotブログ）
特徴量ごとの作用を使ってモデルの中身を解釈する（DataRobotブログ）
XEMP Prediction Explanations with DataRobot（DataRobotホワイトペーパー、英語）
SHAP値を用いた特徴量のインパクト・予測の説明（DataRobotコミュニティ、動画での操作説明）

外部ブログ等

オンデマンドビデオ

AI Experience Virtual Conference 2021

「DataRobot AI Cloud」に関する基調講演や、業界をリードするDX推進企業の取り組み、AIサクセスを実現するビジネスリーダーによるパネルセッションをオンデマンドビデオで確認

オンデマンドで見る

執筆者について

川越雄介（Yusuke Kawagoe）

シニアデータサイエンティスト

DataRobot シニアデータサイエンティスト。2019年から DataRobot にて活動。10年以上、ガス会社で機械設備の技術開発に携わった経験を活かし、電気や機械が分かるデータサイエンティストとして、主に製造業・ユーティリティー企業様の AI 活用推進を支援している。現在も名古屋市に居住しており、中部地方や西日本のお客様を中心にサポート。

川越雄介（Yusuke Kawagoe）についてもっとくわしく

投稿をシェアする